Lagrange

Click here to read what the information on this page means.

Alternative names	Polynomial, Galerkin, DGT (facets), Hdiv trace (facets), Q (quadrilateral and hexahedron), Gauss–Lobatto–Legendre (GLL variant), Lobatto (Lobatto variant)
De Rham complex families	\(\left[S_{2,k}^\unicode{0x25FA}\right]_{0}\) / \(\mathcal{P}^-_{k}\Lambda^{0}(\Delta_d)\), \(\left[S_{1,k}^\unicode{0x25FA}\right]_{0}\) / \(\mathcal{P}_{k}\Lambda^{0}(\Delta_d)\), \(\left[S_{4,k}^\square\right]_{0}\) / \(\mathcal{Q}^-_{k}\Lambda^{0}(\square_d)\), \(\left[S_{2,k}^\unicode{0x25FA}\right]_{d}\) / \(\mathcal{P}^-_{k}\Lambda^{d}(\Delta_d)\), \(\left[S_{1,k}^\unicode{0x25FA}\right]_{d}\) / \(\mathcal{P}_{k}\Lambda^{d}(\Delta_d)\), \(\left[S_{4,k}^\square\right]_{d}\) / \(\mathcal{Q}^-_{k}\Lambda^{d}(\square_d)\), \(\left[S_{3,k}^\square\right]_{d}\)
Abbreviated names	P, CG, DG, GLL (GLL variant)
Variants	equispaced: The variant has its point evaluations at equally spaced points. GLL: This variant has its point evaluations at GLL points. Lobatto: This variant uses integrals against L2 duals of Lobatto polynomials in the place of point evaluations
Orders	\(1\leqslant k\)
Reference elements	interval, triangle, tetrahedron, quadrilateral, hexahedron, prism, pyramid
Polynomial set	\(\mathcal{P}_{k}\) (interval, triangle, tetrahedron) \(\mathcal{Q}_{k}\) (quadrilateral, hexahedron) \(\mathcal{Z}^{(15)}_{k}\) (prism) \(\mathcal{Z}^{(16)}_{k} \oplus \mathcal{Z}^{(17)}_{k}\) (pyramid) ↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑ \(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\sum_{i=1}^dp_i\leqslant k\right\}\) \(\mathcal{Q}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\max_i(p_i)\leqslant k\right\}\) \(\mathcal{Z}^{(15)}_k=\operatorname{span}\left\{x_1^{p_1}x_2^{p_2}x_3^{p_3}\middle\|\max(p_1+p_2,p_3)\leqslant k\right\}\) \(\mathcal{Z}^{(16)}_k=\operatorname{span}\left\{x_1^{p_1}x_2^{p_2}x_3^{p_3}\middle\|p_3\leqslant k-1,p_1+p_3\leqslant k,p_2+p_3\leqslant k\right\}\) \(\mathcal{Z}^{(17)}_k=\operatorname{span}\left\{x_3^k\right\}\)
DOFs	On each vertex: point evaluations On each edge: point evaluations On each face: point evaluations On each volume: point evaluations
Number of DOFs	interval: \(k+1\) (A000027) triangle: \((k+1)(k+2)/2\) (A000217) tetrahedron: \((k+1)(k+2)(k+3)/6\) (A000292) quadrilateral: \((k+1)^2\) (A000290) hexahedron: \((k+1)^3\) (A000578) prism: \((k+1)^2(k+2)/2\) (A002411) pyramid: \((k+1)(k+2)(2k+3)/6\) (A000330)
Number of DOFs on subentities	vertices: \(1\) (A000012) edges: \(k-1\) (A000027) faces: \((k-1)(k-2)/2\) (A000217) (triangle), \((k-1)^2\) (A000290) (quadrilateral) volumes: \((k-1)(k-2)(k-3)/6\) (A000292) (tetrahedron), \((k-1)^3\) (A000578) (hexahedron), \((k-1)^2(k-2)/2\) (A002411) (prism), \((k-1)(k-2)(2k-3)/6\) (A000330) (pyramid)
Mapping	identity
continuity	Function values are continuous.
Notes	DGT and Hdiv trace are names given to this element when it is defined on the facets of a mesh. For the Lobatto variant, the derivatives of most of the basis functions are orthogonal.
Categories	Scalar-valued elements

Implementations

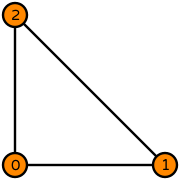
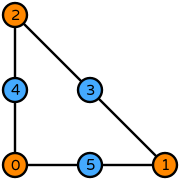
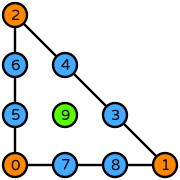
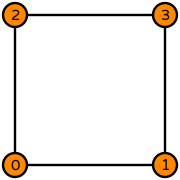
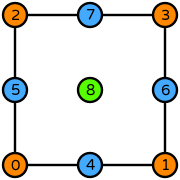
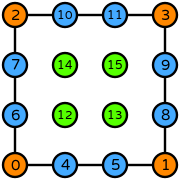
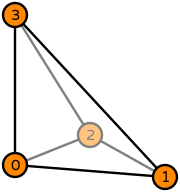
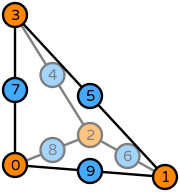
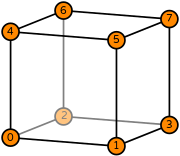
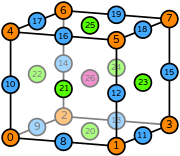
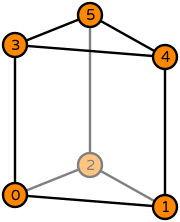
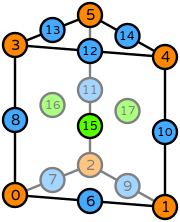
Basix	`basix.ElementFamily.P` ↓ Show Basix examples ↓↑ Hide Basix examples ↑ Before trying this example, you must install Basix: pip3 install git+https://github.com/FEniCS/basix.git This element can then be created with the following lines of Python: import basix # Create Lagrange (equispaced variant) order 1 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 3 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a triangle element = basix.create_element(basix.ElementFamily.P, basix.CellType.triangle, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a triangle element = basix.create_element(basix.ElementFamily.P, basix.CellType.triangle, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 3 on a triangle element = basix.create_element(basix.ElementFamily.P, basix.CellType.triangle, 3, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a quadrilateral element = basix.create_element(basix.ElementFamily.P, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a quadrilateral element = basix.create_element(basix.ElementFamily.P, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 3 on a quadrilateral element = basix.create_element(basix.ElementFamily.P, basix.CellType.quadrilateral, 3, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a tetrahedron element = basix.create_element(basix.ElementFamily.P, basix.CellType.tetrahedron, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a tetrahedron element = basix.create_element(basix.ElementFamily.P, basix.CellType.tetrahedron, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a hexahedron element = basix.create_element(basix.ElementFamily.P, basix.CellType.hexahedron, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a hexahedron element = basix.create_element(basix.ElementFamily.P, basix.CellType.hexahedron, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a prism element = basix.create_element(basix.ElementFamily.P, basix.CellType.prism, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a prism element = basix.create_element(basix.ElementFamily.P, basix.CellType.prism, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (GLL variant) order 1 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 2 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 3 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 4 on a interval element = basix.create_element(basix.ElementFamily.P, basix.CellType.interval, 4, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 1 on a quadrilateral element = basix.create_element(basix.ElementFamily.P, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 2 on a quadrilateral element = basix.create_element(basix.ElementFamily.P, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.gll_warped) This implementation is correct for all the examples below that it supports. ↓ Show more ↓ ↑ Hide ↑ Correct: interval,1,equispaced; interval,2,equispaced; interval,3,equispaced; triangle,1,equispaced; triangle,2,equispaced; triangle,3,equispaced; quadrilateral,1,equispaced; quadrilateral,2,equispaced; quadrilateral,3,equispaced; tetrahedron,1,equispaced; tetrahedron,2,equispaced; hexahedron,1,equispaced; hexahedron,2,equispaced; prism,1,equispaced; prism,2,equispaced; interval,1,gll; interval,2,gll; interval,3,gll; interval,4,gll; quadrilateral,1,gll; quadrilateral,2,gll Not implemented: pyramid,1,equispaced; pyramid,2,equispaced; interval,1,lobatto; interval,2,lobatto; interval,3,lobatto; quadrilateral,1,lobatto; quadrilateral,2,lobatto; quadrilateral,3,lobatto; hexahedron,1,lobatto; hexahedron,2,lobatto
Basix.UFL	`basix.ElementFamily.P` ↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑ Before trying this example, you must install Basix.UFL: pip3 install git+https://github.com/FEniCS/basix.git git+https://github.com/FEniCS/ufl.git This element can then be created with the following lines of Python: import basix import basix.ufl # Create Lagrange (equispaced variant) order 1 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 3 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a triangle element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.triangle, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a triangle element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.triangle, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 3 on a triangle element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.triangle, 3, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 3 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 3, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a tetrahedron element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.tetrahedron, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a tetrahedron element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.tetrahedron, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a hexahedron element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.hexahedron, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a hexahedron element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.hexahedron, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 1 on a prism element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.prism, 1, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (equispaced variant) order 2 on a prism element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.prism, 2, lagrange_variant=basix.LagrangeVariant.equispaced) # Create Lagrange (GLL variant) order 1 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 2 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 3 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 4 on a interval element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.interval, 4, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 1 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.gll_warped) # Create Lagrange (GLL variant) order 2 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.gll_warped) This implementation is correct for all the examples below that it supports. ↓ Show more ↓ ↑ Hide ↑ Correct: interval,1,equispaced; interval,2,equispaced; interval,3,equispaced; triangle,1,equispaced; triangle,2,equispaced; triangle,3,equispaced; quadrilateral,1,equispaced; quadrilateral,2,equispaced; quadrilateral,3,equispaced; tetrahedron,1,equispaced; tetrahedron,2,equispaced; hexahedron,1,equispaced; hexahedron,2,equispaced; prism,1,equispaced; prism,2,equispaced; interval,1,gll; interval,2,gll; interval,3,gll; interval,4,gll; quadrilateral,1,gll; quadrilateral,2,gll Not implemented: pyramid,1,equispaced; pyramid,2,equispaced; interval,1,lobatto; interval,2,lobatto; interval,3,lobatto; quadrilateral,1,lobatto; quadrilateral,2,lobatto; quadrilateral,3,lobatto; hexahedron,1,lobatto; hexahedron,2,lobatto
Bempp	`"P"` ↓ Show Bempp examples ↓↑ Hide Bempp examples ↑ Before trying this example, you must install Bempp: pip3 install bempp-cl This element can then be created with the following lines of Python: import bempp.api grid = bempp.api.shapes.regular_sphere(1) # Create Lagrange order 1 element = bempp.api.function_space(grid, "P", 1)
FIAT	`FIAT.Lagrange` ↓ Show FIAT examples ↓↑ Hide FIAT examples ↑ Before trying this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT # Create Lagrange (equispaced variant) order 1 element = FIAT.Lagrange(FIAT.ufc_cell("interval"), 1) # Create Lagrange (equispaced variant) order 2 element = FIAT.Lagrange(FIAT.ufc_cell("interval"), 2) # Create Lagrange (equispaced variant) order 3 element = FIAT.Lagrange(FIAT.ufc_cell("interval"), 3) # Create Lagrange (equispaced variant) order 1 element = FIAT.Lagrange(FIAT.ufc_cell("triangle"), 1) # Create Lagrange (equispaced variant) order 2 element = FIAT.Lagrange(FIAT.ufc_cell("triangle"), 2) # Create Lagrange (equispaced variant) order 3 element = FIAT.Lagrange(FIAT.ufc_cell("triangle"), 3) # Create Lagrange (equispaced variant) order 1 element = FIAT.Lagrange(FIAT.ufc_cell("tetrahedron"), 1) # Create Lagrange (equispaced variant) order 2 element = FIAT.Lagrange(FIAT.ufc_cell("tetrahedron"), 2) This implementation is correct for all the examples below that it supports. ↓ Show more ↓ ↑ Hide ↑ Correct: interval,1,equispaced; interval,2,equispaced; interval,3,equispaced; triangle,1,equispaced; triangle,2,equispaced; triangle,3,equispaced; tetrahedron,1,equispaced; tetrahedron,2,equispaced Not implemented: quadrilateral,1,equispaced; quadrilateral,2,equispaced; quadrilateral,3,equispaced; hexahedron,1,equispaced; hexahedron,2,equispaced; prism,1,equispaced; prism,2,equispaced; pyramid,1,equispaced; pyramid,2,equispaced; interval,1,gll; interval,2,gll; interval,3,gll; interval,4,gll; quadrilateral,1,gll; quadrilateral,2,gll; interval,1,lobatto; interval,2,lobatto; interval,3,lobatto; quadrilateral,1,lobatto; quadrilateral,2,lobatto; quadrilateral,3,lobatto; hexahedron,1,lobatto; hexahedron,2,lobatto
Symfem	`"Lagrange"` (interval, equispaced; triangle, equispaced; tetrahedron, equispaced; prism, equispaced; pyramid, equispaced) `"Q"` (quadrilateral, equispaced; hexahedron, equispaced) `"Lagrange", variant="gll"` (interval, GLL) `"Q", variant="gll"` (quadrilateral, GLL; hexahedron, GLL) `"Lagrange", variant="lobatto"` (interval, Lobatto) `"Q", variant="lobatto"` (quadrilateral, Lobatto; hexahedron, Lobatto) ↓ Show Symfem examples ↓↑ Hide Symfem examples ↑ Before trying this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem # Create Lagrange (equispaced variant) order 1 on a interval element = symfem.create_element("interval", "Lagrange", 1) # Create Lagrange (equispaced variant) order 2 on a interval element = symfem.create_element("interval", "Lagrange", 2) # Create Lagrange (equispaced variant) order 3 on a interval element = symfem.create_element("interval", "Lagrange", 3) # Create Lagrange (equispaced variant) order 1 on a triangle element = symfem.create_element("triangle", "Lagrange", 1) # Create Lagrange (equispaced variant) order 2 on a triangle element = symfem.create_element("triangle", "Lagrange", 2) # Create Lagrange (equispaced variant) order 3 on a triangle element = symfem.create_element("triangle", "Lagrange", 3) # Create Lagrange (equispaced variant) order 1 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 1) # Create Lagrange (equispaced variant) order 2 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 2) # Create Lagrange (equispaced variant) order 3 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 3) # Create Lagrange (equispaced variant) order 1 on a tetrahedron element = symfem.create_element("tetrahedron", "Lagrange", 1) # Create Lagrange (equispaced variant) order 2 on a tetrahedron element = symfem.create_element("tetrahedron", "Lagrange", 2) # Create Lagrange (equispaced variant) order 1 on a hexahedron element = symfem.create_element("hexahedron", "Q", 1) # Create Lagrange (equispaced variant) order 2 on a hexahedron element = symfem.create_element("hexahedron", "Q", 2) # Create Lagrange (equispaced variant) order 1 on a prism element = symfem.create_element("prism", "Lagrange", 1) # Create Lagrange (equispaced variant) order 2 on a prism element = symfem.create_element("prism", "Lagrange", 2) # Create Lagrange (equispaced variant) order 1 on a pyramid element = symfem.create_element("pyramid", "Lagrange", 1) # Create Lagrange (equispaced variant) order 2 on a pyramid element = symfem.create_element("pyramid", "Lagrange", 2) # Create Lagrange (GLL variant) order 1 on a interval element = symfem.create_element("interval", "Lagrange", 1, variant="gll") # Create Lagrange (GLL variant) order 2 on a interval element = symfem.create_element("interval", "Lagrange", 2, variant="gll") # Create Lagrange (GLL variant) order 3 on a interval element = symfem.create_element("interval", "Lagrange", 3, variant="gll") # Create Lagrange (GLL variant) order 4 on a interval element = symfem.create_element("interval", "Lagrange", 4, variant="gll") # Create Lagrange (GLL variant) order 1 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 1, variant="gll") # Create Lagrange (GLL variant) order 2 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 2, variant="gll") # Create Lagrange (Lobatto variant) order 1 on a interval element = symfem.create_element("interval", "Lagrange", 1, variant="lobatto") # Create Lagrange (Lobatto variant) order 2 on a interval element = symfem.create_element("interval", "Lagrange", 2, variant="lobatto") # Create Lagrange (Lobatto variant) order 3 on a interval element = symfem.create_element("interval", "Lagrange", 3, variant="lobatto") # Create Lagrange (Lobatto variant) order 1 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 1, variant="lobatto") # Create Lagrange (Lobatto variant) order 2 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 2, variant="lobatto") # Create Lagrange (Lobatto variant) order 3 on a quadrilateral element = symfem.create_element("quadrilateral", "Q", 3, variant="lobatto") # Create Lagrange (Lobatto variant) order 1 on a hexahedron element = symfem.create_element("hexahedron", "Q", 1, variant="lobatto") # Create Lagrange (Lobatto variant) order 2 on a hexahedron element = symfem.create_element("hexahedron", "Q", 2, variant="lobatto") This implementation is used to compute the examples below and verify other implementations.
(legacy) UFL	`"Lagrange"` (interval, equispaced; triangle, equispaced; tetrahedron, equispaced) `"Q"` (quadrilateral, equispaced; hexahedron, equispaced) `"Lobatto"` (interval, Lobatto) ↓ Show (legacy) UFL examples ↓↑ Hide (legacy) UFL examples ↑ Before trying this example, you must install (legacy) UFL: pip3 install fenics-ufl-legacy This element can then be created with the following lines of Python: import ufl_legacy # Create Lagrange (equispaced variant) order 1 on a interval element = ufl_legacy.FiniteElement("Lagrange", "interval", 1) # Create Lagrange (equispaced variant) order 2 on a interval element = ufl_legacy.FiniteElement("Lagrange", "interval", 2) # Create Lagrange (equispaced variant) order 3 on a interval element = ufl_legacy.FiniteElement("Lagrange", "interval", 3) # Create Lagrange (equispaced variant) order 1 on a triangle element = ufl_legacy.FiniteElement("Lagrange", "triangle", 1) # Create Lagrange (equispaced variant) order 2 on a triangle element = ufl_legacy.FiniteElement("Lagrange", "triangle", 2) # Create Lagrange (equispaced variant) order 3 on a triangle element = ufl_legacy.FiniteElement("Lagrange", "triangle", 3) # Create Lagrange (equispaced variant) order 1 on a quadrilateral element = ufl_legacy.FiniteElement("Q", "quadrilateral", 1) # Create Lagrange (equispaced variant) order 2 on a quadrilateral element = ufl_legacy.FiniteElement("Q", "quadrilateral", 2) # Create Lagrange (equispaced variant) order 3 on a quadrilateral element = ufl_legacy.FiniteElement("Q", "quadrilateral", 3) # Create Lagrange (equispaced variant) order 1 on a tetrahedron element = ufl_legacy.FiniteElement("Lagrange", "tetrahedron", 1) # Create Lagrange (equispaced variant) order 2 on a tetrahedron element = ufl_legacy.FiniteElement("Lagrange", "tetrahedron", 2) # Create Lagrange (equispaced variant) order 1 on a hexahedron element = ufl_legacy.FiniteElement("Q", "hexahedron", 1) # Create Lagrange (equispaced variant) order 2 on a hexahedron element = ufl_legacy.FiniteElement("Q", "hexahedron", 2) # Create Lagrange (Lobatto variant) order 1 on a interval element = ufl_legacy.FiniteElement("Lobatto", "interval", 1) # Create Lagrange (Lobatto variant) order 2 on a interval element = ufl_legacy.FiniteElement("Lobatto", "interval", 2) # Create Lagrange (Lobatto variant) order 3 on a interval element = ufl_legacy.FiniteElement("Lobatto", "interval", 3)

Examples

interval order 1 equispaced variant	(click to view basis functions)
interval order 2 equispaced variant	(click to view basis functions)
interval order 3 equispaced variant	(click to view basis functions)
triangle order 1 equispaced variant	(click to view basis functions)
triangle order 2 equispaced variant	(click to view basis functions)
triangle order 3 equispaced variant	(click to view basis functions)
quadrilateral order 1 equispaced variant	(click to view basis functions)
quadrilateral order 2 equispaced variant	(click to view basis functions)
quadrilateral order 3 equispaced variant	(click to view basis functions)
tetrahedron order 1 equispaced variant	(click to view basis functions)
tetrahedron order 2 equispaced variant	(click to view basis functions)
hexahedron order 1 equispaced variant	(click to view basis functions)
hexahedron order 2 equispaced variant	(click to view basis functions)
prism order 1 equispaced variant	(click to view basis functions)
prism order 2 equispaced variant	(click to view basis functions)
pyramid order 1 equispaced variant	(click to view basis functions)
pyramid order 2 equispaced variant	(click to view basis functions)
interval order 1 GLL variant	(click to view basis functions)
interval order 2 GLL variant	(click to view basis functions)
interval order 3 GLL variant	(click to view basis functions)
interval order 4 GLL variant	(click to view basis functions)
quadrilateral order 1 GLL variant	(click to view basis functions)
quadrilateral order 2 GLL variant	(click to view basis functions)
interval order 1 Lobatto variant	(click to view basis functions)
interval order 2 Lobatto variant	(click to view basis functions)
interval order 3 Lobatto variant	(click to view basis functions)
quadrilateral order 1 Lobatto variant	(click to view basis functions)
quadrilateral order 2 Lobatto variant	(click to view basis functions)
quadrilateral order 3 Lobatto variant	(click to view basis functions)
hexahedron order 1 Lobatto variant	(click to view basis functions)
hexahedron order 2 Lobatto variant	(click to view basis functions)

References

Arnold, Douglas N. and Logg, Anders. Periodic table of the finite elements, SIAM News 47, 2014. [sinews.siam.org/Details-Page/periodic-table-of-the-finite-elements] [BibTeX]
Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM journal on numerical analysis 55, 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]

DefElement stats

Element added	09 January 2021
Element last updated	12 December 2023