an encyclopedia of finite element definitions
Guzmán–Neilan
Click here to read what the information on this page means.
| Abbreviated names | BR |
| Orders | \(k=1\) |
| Reference elements | triangle, tetrahedron |
| DOFs | On each edge: (if \(k>1\)) point evaluations in tangential directions at midpoints On each facet: point evaluations in normal directions at vertices, normal integral moments with an order \(k-1\) Lagrange space, and (if \(k>1\)) point evaluations in normal directions at midpoints of edges On the interior of the reference element: , and point evaluations at the midpoint |
| Number of DOFs | triangle: \(11\) tetrahedron: \(\begin{cases}19&k=1\\49&k=2\end{cases}\) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Notes | This element is a modification of the Bernardi–Raugel element with the facet bubbles modified to be divergence free. |
| Categories | Vector-valued elements, H(div) conforming elements, Macro elements |
Implementations
"Guzman-Neilan"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| triangle order 1 | 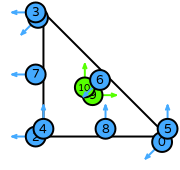 (click to view basis functions) |
| tetrahedron order 1 | 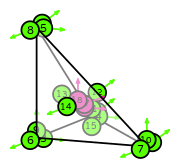 (click to view basis functions) |
| tetrahedron order 2 | 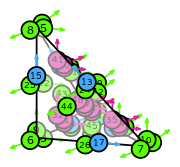 (click to view basis functions) |
References
- Guzmán, Johnny and Neilan, Michael. Inf-sup stable finite elements on barycentric refinements producing divergence-free approximations in arbitrary dimensions, SIAM Journal on Numerical Analysis 56, 2826–2844, 2018. [DOI: 10.1137/17M1153467] [BibTeX]
DefElement stats
| Element added | 01 August 2021 |
| Element last updated | 16 September 2023 |