Brezzi–Douglas–Fortin–Marini
Click here to read what the information on this page means.
| Abbreviated names | BDFM |
| Orders | \(1\leqslant k\) |
| Reference elements | triangle, quadrilateral, tetrahedron, hexahedron |
| Polynomial set | \(\mathcal{Z}^{(10)}_{k}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each facet: normal integral moments with an order \(k-1\) Lagrange space On the interior of the reference element: integral moments with an order \(k-2\) vector Lagrange space |
| Number of DOFs | triangle: \(k(k+2)\) quadrilateral: \(k(k+3)\) (A028552) tetrahedron: \(k(k+1)(k+3)/2\) hexahedron: \(k(k+1)(k+5)/2\) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
Implementations
FIAT.BrezziDouglasFortinMarini↓ Show FIAT examples ↓ This implementation is correct for all the examples below. | |
"BDFM"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. | |
"BDFM"↓ Show (legacy) UFL examples ↓ |
Examples
| triangle order 1 | 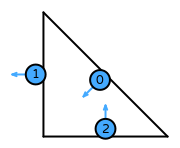 (click to view basis functions) |
| triangle order 2 | 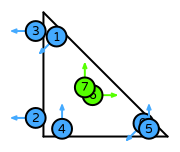 (click to view basis functions) |
| quadrilateral order 1 | 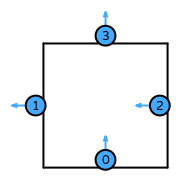 (click to view basis functions) |
| quadrilateral order 2 | 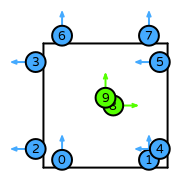 (click to view basis functions) |
| tetrahedron order 2 | 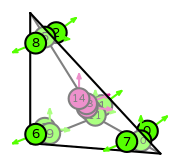 (click to view basis functions) |
| hexahedron order 2 | 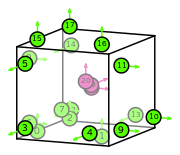 (click to view basis functions) |
References
- Brezzi, Franco, Douglas, Jim, Fortin, Michel, and Marini, L. Donatella. Efficient rectangular mixed finite elements in two and three space variables, ESAIM: Mathematical Modelling and Numerical Analysis 21, 581–604, 1987. [DOI: 10.1051/m2an/1987210405811] [BibTeX]
DefElement stats
| Element added | 30 January 2021 |
| Element last updated | 16 September 2023 |