an encyclopedia of finite element definitions
Arnold–Boffi–Falk
Click here to read what the information on this page means.
| Abbreviated names | ABF |
| Degrees | \(0\leqslant k\) where \(k\) is the Polynomial subdegree |
| Polynomial subdegree | \(k\) |
| Polynomial superdegree | \(2k+2\) |
| Lagrange subdegree | \(k\) |
| Lagrange superdegree | \(k+2\) |
| Reference elements | quadrilateral |
| Polynomial set | \(\mathcal{Z}^{(0)}_{k} \oplus \mathcal{Z}^{(1)}_{k}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each edge: normal integral moments with an degree \(k\) Lagrange space On each face: integral moments with an degree \(k\) Nédélec (first kind) space, integral moments of the divergence with \(x^{k+1}y^q\) for q=0,1,...,k, and integral moments of the divergence with \(x^qy^{k+1}\) for q=0,1,...,k |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
Implementations
This element is implemented in Symfem .↓ Show implementation detail ↓Examples
| quadrilateral degree 0 | 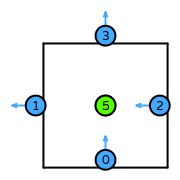 (click to view basis functions) |
| quadrilateral degree 1 | 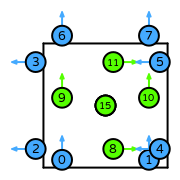 (click to view basis functions) |
| quadrilateral degree 2 | 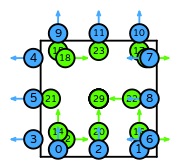 (click to view basis functions) |
References
- Arnold, Douglas N., Boffi, Daniele, and Falk, Richard S. Quadrilateral H(div) finite elements, SIAM Journal on Numerical Analysis 42(5), 2429–2451, 2005. [DOI: 10.1137/S0036142903431924] [BibTeX]
DefElement stats
| Element added | 01 December 2021 |
| Element last updated | 27 September 2024 |