an encyclopedia of finite element definitions
Tiniest tensor
Click here to read what the information on this page means.
| Alternative names | TNT |
| De Rham complex families | \(\left[S_{3,k}^\square\right]_{0}\) |
| Orders | \(1\leqslant k\) |
| Reference elements | quadrilateral, hexahedron |
| Polynomial set | \(\mathcal{Q}_{k} \oplus \mathcal{Z}^{(30)}_{k}\) (quadrilateral) \(\mathcal{Q}_{k} \oplus \mathcal{Z}^{(31)}_{k} \oplus \mathcal{Z}^{(32)}_{k} \oplus \mathcal{Z}^{(33)}_{k}\) (hexahedron) ↓ Show polynomial set definitions ↓ |
| DOFs | On each vertex: point evaluations On each edge: integral moments with \(\frac{\partial}{\partial x}f\) for each \(f\) in an order \(k\) Lagrange space On each face: integral moments with \(\Delta f\) for each \(f\) in an order \(k\) Lagrange space such that the trace of \(f\) on the edges of the face is 0 On each volume: integral moments of gradient with \(\nabla f\) for each \(f\) in an order \(k\) Lagrange space such that the trace of \(f\) on the faces of the volume is 0 |
| Number of DOFs | quadrilateral: \((k+1)^2 + 4\) hexahedron: \((k+1)^3 + 12\) |
| Mapping | identity |
| continuity | Function values are continuous. |
| Categories | Scalar-valued elements |
Implementations
"TNT"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| quadrilateral order 1 | 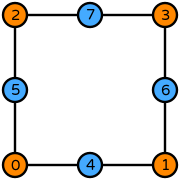 (click to view basis functions) |
| quadrilateral order 2 | 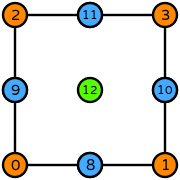 (click to view basis functions) |
| quadrilateral order 3 |  (click to view basis functions) |
| hexahedron order 1 | 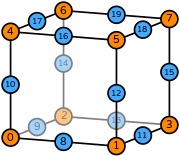 (click to view basis functions) |
References
- Cockburn, Bernardo and Qiu, Weifeng. Commuting diagrams for the TNT elements on cubes, Mathematics of Computation 83, 603–633, 2014. [DOI: 10.1090/S0025-5718-2013-02729-9] [BibTeX]
- Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM journal on numerical analysis 55, 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]
DefElement stats
| Element added | 24 October 2021 |
| Element last updated | 16 September 2023 |