Click here to read what the information on this page means.
| Alternative names | TNT H(div) |
| De Rham complex families | \(\left[S_{3,k}^\square\right]_{d-1}\) |
| Orders | \(1\leqslant k\) |
| Reference elements | quadrilateral, hexahedron |
| Polynomial set | \(\mathcal{Q}_{k}^d \oplus \mathcal{Z}^{(38)}_{k}\) (quadrilateral)
\(\mathcal{Q}_{k}^d \oplus \mathcal{Z}^{(39)}_{k}\) (hexahedron)
↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑\(\mathcal{Q}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|\max_i(p_i)\leqslant k\right\}\) \(\mathcal{Z}^{(38)}_k=\left\{\left(\begin{array}{c}\tilde{B}_{k+1}(x)\tilde{P}_{k}(y)\\\tilde{P}_k(x)\tilde{B}_{k+1}(y)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(0)\tilde{P}_{k}(y)\\\tilde{P}_k(0)\tilde{B}_{k+1}(y)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(x)\tilde{P}_{k}(0)\\\tilde{P}_k(x)\tilde{B}_{k+1}(0)\end{array}\right)\right\} \) where - \(\tilde{P}_k\) is the degree \(k\) Legendre polynomial on \([0,1]\)
- \(\tilde{B}_k\) is \((\tilde{P}_k-\tilde{P}_{k-2})/(4k-2)\)
\(\mathcal{Z}^{(39)}_k=\left\{\left(\begin{array}{c}\tilde{B}_{k+1}(x)\tilde{P}_{k}(y)\tilde{P}_{k}(z)\\\tilde{P}_k(x)\tilde{B}_{k+1}(y)\tilde{P}_{k}(z)\\\tilde{P}_{k}(x)\tilde{P}_{k}(y)\tilde{B}_{k+1}(z)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(x)\tilde{P}_{k}(y)\tilde{P}_{k}(0)\\\tilde{P}_k(x)\tilde{B}_{k+1}(y)\tilde{P}_{k}(0)\\\tilde{P}_{k}(x)\tilde{P}_{k}(y)\tilde{B}_{k+1}(0)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(x)\tilde{P}_{k}(0)\tilde{P}_{k}(z)\\\tilde{P}_k(x)\tilde{B}_{k+1}(0)\tilde{P}_{k}(z)\\\tilde{P}_{k}(x)\tilde{P}_{k}(0)\tilde{B}_{k+1}(z)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(x)\tilde{P}_{k}(0)\tilde{P}_{k}(0)\\\tilde{P}_k(x)\tilde{B}_{k+1}(0)\tilde{P}_{k}(0)\\\tilde{P}_{k}(x)\tilde{P}_{k}(0)\tilde{B}_{k+1}(0)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(0)\tilde{P}_{k}(y)\tilde{P}_{k}(z)\\\tilde{P}_k(0)\tilde{B}_{k+1}(y)\tilde{P}_{k}(z)\\\tilde{P}_{k}(0)\tilde{P}_{k}(y)\tilde{B}_{k+1}(z)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(0)\tilde{P}_{k}(y)\tilde{P}_{k}(0)\\\tilde{P}_k(0)\tilde{B}_{k+1}(y)\tilde{P}_{k}(0)\\\tilde{P}_{k}(0)\tilde{P}_{k}(y)\tilde{B}_{k+1}(0)\end{array}\right),\left(\begin{array}{c}\tilde{B}_{k+1}(0)\tilde{P}_{k}(0)\tilde{P}_{k}(z)\\\tilde{P}_k(0)\tilde{B}_{k+1}(0)\tilde{P}_{k}(z)\\\tilde{P}_{k}(0)\tilde{P}_{k}(0)\tilde{B}_{k+1}(z)\end{array}\right)\right\} \) where - \(\tilde{P}_k\) is the degree \(k\) Legendre polynomial on \([0,1]\)
- \(\tilde{B}_k\) is \((\tilde{P}_k-\tilde{P}_{k-2})/(4k-2)\)
|
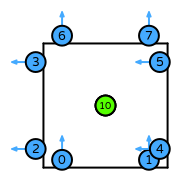
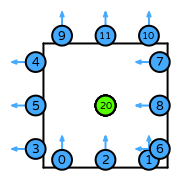
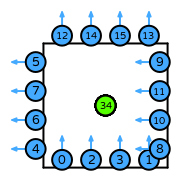
| DOFs | On each facet: normal integral moments with an order \(k\) Lagrange space
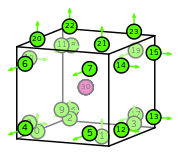
On the interior of the reference element: integral moments with \(\nabla f\) for each \(f\) in an order \(k\) Lagrange space, and integral moments with \(\nabla\times\boldsymbol{f}\) for each \(\boldsymbol{f}\) in an order \(k\) vector Lagrange space such that the tangential trace of \(\boldsymbol{f}\) on the facets of the cell is 0 |
| Number of DOFs | quadrilateral: \(2(k+1)^2 + 3\)
hexahedron: \(3(k+1)^3 + 7\) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
| Symfem | "TNTdiv"
↓ Show Symfem examples ↓↑ Hide Symfem examples ↑Before trying this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem
# Create Tiniest tensor H(div) order 1 on a quadrilateral
element = symfem.create_element("quadrilateral", "TNTdiv", 1)
# Create Tiniest tensor H(div) order 2 on a quadrilateral
element = symfem.create_element("quadrilateral", "TNTdiv", 2)
# Create Tiniest tensor H(div) order 3 on a quadrilateral
element = symfem.create_element("quadrilateral", "TNTdiv", 3)
# Create Tiniest tensor H(div) order 1 on a hexahedron
element = symfem.create_element("hexahedron", "TNTdiv", 1) |
- Cockburn, Bernardo and Qiu, Weifeng. Commuting diagrams for the TNT elements on cubes, Mathematics of Computation 83, 603–633, 2014. [DOI: 10.1090/S0025-5718-2013-02729-9] [BibTeX]
- Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM journal on numerical analysis 55, 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]
| Element added | 24 October 2021 |
| Element last updated | 16 September 2023 |