| Alternative names | Rao–Wilton–Glisson, Nédélec (first kind) H(div) |
| De Rham complex families | \(\left[S_{2,k}^\unicode{0x25FA}\right]_{d-1}\) / \(\mathcal{P}^-_{k}\Lambda^{d-1}(\Delta_d)\) |
| Abbreviated names | RT, RWG |
| Variants | Legendre: Integral moments are taken against orthonormal polynomials
Lagrange: Integral moments are taken against (Lagrange)[element:lagrange] basis functions |
| Orders | \(1\leqslant k\) |
| Reference elements | triangle, tetrahedron |
| Polynomial set | \(\mathcal{P}_{k-1}^d \oplus \mathcal{Z}^{(25)}_{k}\)
↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑\(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|\sum_{i=1}^dp_i\leqslant k\right\}\)
\(\mathcal{Z}^{(25)}_k=\left\{\left(\begin{array}{c}px_1\\\vdots\\px_d\end{array}\right)\middle|p\in\hat{\mathcal{P}}_{k-1}\right\}\)
\(\hat{\mathcal{P}}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|\sum_{i=1}^dp_i=k\right\}=\mathcal{P}_k\setminus\mathcal{P}_{k-1}\) |
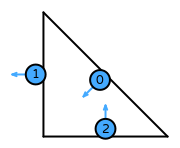
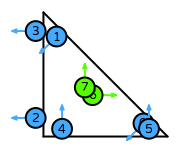
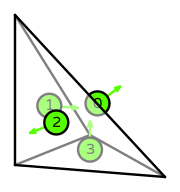
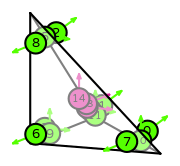
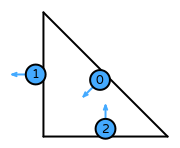
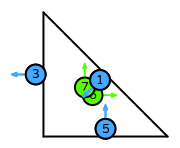
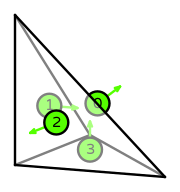
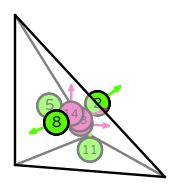
| DOFs | On each facet: normal integral moments with an order \(k-1\) Lagrange space
On the interior of the reference element: integral moments with an order \(k-2\) vector Lagrange space |
| Number of DOFs | triangle: \(k(k+2)\) (A005563)
tetrahedron: \(k(k+1)(k+3)/2\) (A077414) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
| Basix | basix.ElementFamily.RT
↓ Show Basix examples ↓↑ Hide Basix examples ↑Before trying this example, you must install Basix: pip3 install git+https://github.com/FEniCS/basix.git This element can then be created with the following lines of Python: import basix
# Create Raviart-Thomas (Lagrange variant) order 1 on a triangle
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.triangle, 1)
# Create Raviart-Thomas (Lagrange variant) order 2 on a triangle
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.triangle, 2)
# Create Raviart-Thomas (Lagrange variant) order 1 on a tetrahedron
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 1)
# Create Raviart-Thomas (Lagrange variant) order 2 on a tetrahedron
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 2)
# Create Raviart-Thomas (Legendre variant) order 1 on a triangle
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.triangle, 1, lagrange_variant=basix.LagrangeVariant.legendre)
# Create Raviart-Thomas (Legendre variant) order 2 on a triangle
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.triangle, 2, lagrange_variant=basix.LagrangeVariant.legendre)
# Create Raviart-Thomas (Legendre variant) order 1 on a tetrahedron
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 1, lagrange_variant=basix.LagrangeVariant.legendre)
# Create Raviart-Thomas (Legendre variant) order 2 on a tetrahedron
element = basix.create_element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 2, lagrange_variant=basix.LagrangeVariant.legendre) |
| Basix.UFL | basix.ElementFamily.RT
↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑Before trying this example, you must install Basix.UFL: pip3 install git+https://github.com/FEniCS/basix.git git+https://github.com/FEniCS/ufl.git This element can then be created with the following lines of Python: import basix
import basix.ufl
# Create Raviart-Thomas (Lagrange variant) order 1 on a triangle
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.triangle, 1, lagrange_variant=basix.LagrangeVariant.equispaced)
# Create Raviart-Thomas (Lagrange variant) order 2 on a triangle
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.triangle, 2, lagrange_variant=basix.LagrangeVariant.equispaced)
# Create Raviart-Thomas (Lagrange variant) order 1 on a tetrahedron
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 1, lagrange_variant=basix.LagrangeVariant.equispaced)
# Create Raviart-Thomas (Lagrange variant) order 2 on a tetrahedron
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 2, lagrange_variant=basix.LagrangeVariant.equispaced)
# Create Raviart-Thomas (Legendre variant) order 1 on a triangle
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.triangle, 1)
# Create Raviart-Thomas (Legendre variant) order 2 on a triangle
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.triangle, 2)
# Create Raviart-Thomas (Legendre variant) order 1 on a tetrahedron
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 1)
# Create Raviart-Thomas (Legendre variant) order 2 on a tetrahedron
element = basix.ufl.element(basix.ElementFamily.RT, basix.CellType.tetrahedron, 2) |
| Bempp |
↓ Show Bempp examples ↓↑ Hide Bempp examples ↑Before trying this example, you must install Bempp: pip3 install numba scipy meshio
pip3 install bempp-cl
This element can then be created with the following lines of Python: import bempp.api
grid = bempp.api.shapes.regular_sphere(1) |
| FIAT | FIAT.RaviartThomas(..., variant="integral")
↓ Show FIAT examples ↓↑ Hide FIAT examples ↑Before trying this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT
# Create Raviart-Thomas (Legendre variant) order 1
element = FIAT.RaviartThomas(FIAT.ufc_cell("triangle"), 1, variant="integral")
# Create Raviart-Thomas (Legendre variant) order 2
element = FIAT.RaviartThomas(FIAT.ufc_cell("triangle"), 2, variant="integral")
# Create Raviart-Thomas (Legendre variant) order 1
element = FIAT.RaviartThomas(FIAT.ufc_cell("tetrahedron"), 1, variant="integral")
# Create Raviart-Thomas (Legendre variant) order 2
element = FIAT.RaviartThomas(FIAT.ufc_cell("tetrahedron"), 2, variant="integral") |
| Symfem | "N1div", variant="legendre" (Legendre)
"N1div" (Lagrange)
↓ Show Symfem examples ↓↑ Hide Symfem examples ↑Before trying this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem
# Create Raviart-Thomas (Lagrange variant) order 1 on a triangle
element = symfem.create_element("triangle", "N1div", 1)
# Create Raviart-Thomas (Lagrange variant) order 2 on a triangle
element = symfem.create_element("triangle", "N1div", 2)
# Create Raviart-Thomas (Lagrange variant) order 1 on a tetrahedron
element = symfem.create_element("tetrahedron", "N1div", 1)
# Create Raviart-Thomas (Lagrange variant) order 2 on a tetrahedron
element = symfem.create_element("tetrahedron", "N1div", 2)
# Create Raviart-Thomas (Legendre variant) order 1 on a triangle
element = symfem.create_element("triangle", "N1div", 1, variant="legendre")
# Create Raviart-Thomas (Legendre variant) order 2 on a triangle
element = symfem.create_element("triangle", "N1div", 2, variant="legendre")
# Create Raviart-Thomas (Legendre variant) order 1 on a tetrahedron
element = symfem.create_element("tetrahedron", "N1div", 1, variant="legendre")
# Create Raviart-Thomas (Legendre variant) order 2 on a tetrahedron
element = symfem.create_element("tetrahedron", "N1div", 2, variant="legendre") |
| (legacy) UFL | "RT"
↓ Show (legacy) UFL examples ↓↑ Hide (legacy) UFL examples ↑Before trying this example, you must install (legacy) UFL: pip3 install setuptools
pip3 install fenics-ufl-legacy
This element can then be created with the following lines of Python: import ufl_legacy
# Create Raviart-Thomas (Lagrange variant) order 1 on a triangle
element = ufl_legacy.FiniteElement("RT", "triangle", 1)
# Create Raviart-Thomas (Lagrange variant) order 2 on a triangle
element = ufl_legacy.FiniteElement("RT", "triangle", 2)
# Create Raviart-Thomas (Lagrange variant) order 1 on a tetrahedron
element = ufl_legacy.FiniteElement("RT", "tetrahedron", 1)
# Create Raviart-Thomas (Lagrange variant) order 2 on a tetrahedron
element = ufl_legacy.FiniteElement("RT", "tetrahedron", 2) |