an encyclopedia of finite element definitions
Mardal–Tai–Winther
Click here to read what the information on this page means.
| Abbreviated names | MTW |
| Degrees | \(k=3\) |
| Polynomial subdegree | \(1\) |
| Polynomial superdegree | \(k+d-2\) |
| Reference elements | triangle, tetrahedron |
| Polynomial set | \(\mathcal{Z}^{(17)}_{k}\) (triangle) \(\mathcal{P}_{k}^d \oplus \mathcal{Z}^{(18)}_{k}\) (tetrahedron) ↓ Show polynomial set definitions ↓ |
| DOFs | On each facet (triangle): normal integral moments with an degree \(1\) Lagrange space, and tangent integral moments with an degree \(0\) Lagrange space On each facet (tetrahedron): normal integral moments with an degree \(1\) Lagrange space, and integral moments with an degree \(1\) Nédélec (first kind) space |
| Number of DOFs | triangle: \(9\) tetrahedron: \(24\) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
Implementations
This element is implemented in FIAT , Symfem , and (legacy) UFL.↓ Show implementation detail ↓Examples
| triangle degree 3 | 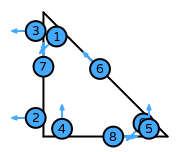 (click to view basis functions) |
| tetrahedron degree 3 | 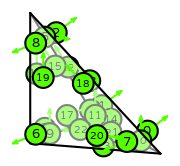 (click to view basis functions) |
References
- Mardal, Kent-Andre, Tai, Xue-Cheng, and Winther, Ragner. A robust finite element method for Darcy–Stokes flow, SIAM Journal on Numerical Analysis 40(5), 1605–1631, 2002. [DOI: 10.1137/S0036142901383910] [BibTeX]
- Tai, Xue-Cheng and Winther, Ragner. A discrete de Rham complex with enhanced smoothness, Calcolo 43, 287–306, 2006. [DOI: 10.1007/s10092-006-0124-6] [BibTeX]
- Kirby, Robert C. A general approach to transforming finite elements, SMAI Journal of Computational Mathematics 4, 197–224, 2018. [DOI: 10.5802/smai-jcm.33] [BibTeX]
DefElement stats
| Element added | 09 January 2021 |
| Element last updated | 27 September 2024 |