an encyclopedia of finite element definitions
Dual polynomial
Click here to read what the information on this page means.
| Abbreviated names | dual |
| Orders | \(0\leqslant k\leqslant 1\) |
| Reference elements | dual polygon |
| Number of DOFs | dual polygon(n): \(\begin{cases}1&k=0\\n&k=1\end{cases}\) |
| Mapping | identity |
| continuity | Discontinuous. (\(n=0\)) Function values are continuous. (\(n=1\)) |
| Notes | These elements are defined on the barycentric dual grid. These elements are defined as a linear combination of Lagrange basis functions on the fine grid. |
| Categories | Scalar-valued elements |
Implementations
"DUAL"↓ Show Bempp examples ↓ | |
"dual"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| dual polygon(6) order 0 | 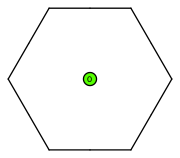 (click to view basis functions) |
| dual polygon(4) order 1 | 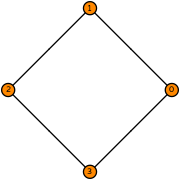 (click to view basis functions) |
| dual polygon(5) order 1 | 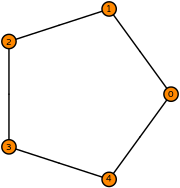 (click to view basis functions) |
| dual polygon(6) order 1 | 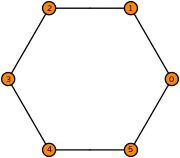 (click to view basis functions) |
References
- Buffa, Annalisa and Christiansen, Snorre H. A dual finite element complex on the barycentric refinement, Mathematics of Computation 76, 1743–1769, 2007. [DOI: 10.1016/j.crma.2004.12.022] [BibTeX]
DefElement stats
| Element added | 24 January 2021 |
| Element last updated | 16 September 2023 |