an encyclopedia of finite element definitions
Degree 0 dual polynomial on a dual polygon
◀ Back to dual polynomial definition page
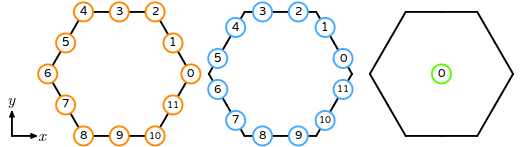
- \(R\) is the reference dual polygon. The following numbering of the subentities of the reference is used:
- Basis functions:
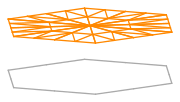
\(\displaystyle \phi_{0} = \begin{cases}
1&\text{in }\operatorname{Triangle}(((0, 0), (1, 0), (3/4, sqrt(3)/4)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (3/4, sqrt(3)/4), (1/2, sqrt(3)/2)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (1/2, sqrt(3)/2), (0, sqrt(3)/2)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (0, sqrt(3)/2), (-1/2, sqrt(3)/2)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (-1/2, sqrt(3)/2), (-3/4, sqrt(3)/4)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (-3/4, sqrt(3)/4), (-1, 0)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (-1, 0), (-3/4, -sqrt(3)/4)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (-3/4, -sqrt(3)/4), (-1/2, -sqrt(3)/2)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (-1/2, -sqrt(3)/2), (0, -sqrt(3)/2)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (0, -sqrt(3)/2), (1/2, -sqrt(3)/2)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (1/2, -sqrt(3)/2), (3/4, -sqrt(3)/4)))\\1&\text{in }\operatorname{Triangle}(((0, 0), (3/4, -sqrt(3)/4), (1, 0)))\end{cases}\)