Trimmed serendipity H(div)
Click here to read what the information on this page means.
| De Rham complex families | \(\left[S_{2,k}^\square\right]_{d-1}\) / \(\mathcal{S}^-_{k}\Lambda^{d-1}(\square_d)\) |
| Orders | \(1\leqslant k\) |
| Reference elements | quadrilateral, hexahedron |
| Polynomial set | \(\mathcal{P}_{k-1}^d \oplus \mathcal{Z}^{(47)}_{k} \oplus \mathcal{Z}^{(48)}_{k}\) (quadrilateral) \(\mathcal{P}_{k-1}^d \oplus \mathcal{Z}^{(47)}_{k} \oplus \mathcal{Z}^{(49)}_{k} \oplus \mathcal{Z}^{(50)}_{k} \oplus \mathcal{Z}^{(51)}_{k}\) (hexahedron) ↓ Show polynomial set definitions ↓ |
| DOFs | On each facet: normal integral moments with an order \(k-1\) dPc space On the interior of the reference element: integral moments with an order \(k-3\) vector dPc space, and integral moments with \(\left\{\nabla(p)\middle|p\text{ is an order \(k-1\) monomial}\right\}\) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
Implementations
FIAT.TrimmedSerendipityDiv↓ Show FIAT examples ↓ This implementation is correct for all the examples below. | |
"TSdiv"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| quadrilateral order 1 |  (click to view basis functions) |
| quadrilateral order 2 |  (click to view basis functions) |
| quadrilateral order 3 | 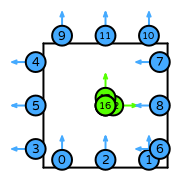 (click to view basis functions) |
| hexahedron order 1 | 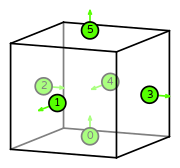 (click to view basis functions) |
| hexahedron order 2 |  (click to view basis functions) |
| hexahedron order 3 |  (click to view basis functions) |
References
- Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM Journal of Numerical Analysis 55(4), 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]
- Gillette, Andrew and Kloefkorn, Tyler. Trimmed serendipity finite element differential forms, Mathematics of Computation 88, 583–606, 2019. [DOI: 10.1090/mcom/3354] [BibTeX]
- Arnold, Douglas N. and Logg, Anders. Periodic table of the finite elements, SIAM News 47, 2014. [sinews.siam.org/Details-Page/periodic-table-of-the-finite-elements] [BibTeX]
- Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM journal on numerical analysis 55, 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]
DefElement stats
| Element added | 07 October 2021 |
| Element last updated | 03 January 2024 |