an encyclopedia of finite element definitions
Transition
Click here to read what the information on this page means.
| Orders | \(1\leqslant k\) |
| Reference elements | triangle, tetrahedron |
| DOFs | On each vertex: point evaluations On each edge: point evaluations On each face: point evaluations On each volume: point evaluations |
| Mapping | identity |
| continuity | Function values are continuous. |
| Notes | This element is used to bridge the gap between Lagrange elements of different orders |
| Categories | Scalar-valued elements |
Implementations
"transition"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| triangle order 1 edge_orders=[2, 1, 1] | 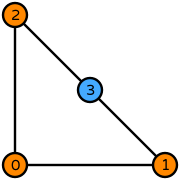 (click to view basis functions) |
| triangle order 1 edge_orders=[3, 2, 1] | 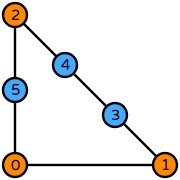 (click to view basis functions) |
| triangle order 3 edge_orders=[1, 1, 1] | 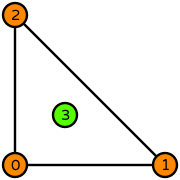 (click to view basis functions) |
DefElement stats
| Element added | 12 July 2021 |
| Element last updated | 16 September 2023 |