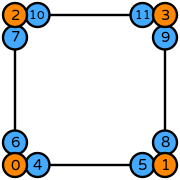
| De Rham complex families | \(\left[S_{1,k}^\square\right]_{0}\) / \(\mathcal{S}_{k}\Lambda^{0}(\square_d)\), \(\left[S_{2,k-d}^\square\right]_{0}\) / \(\mathcal{S}^-_{k-d}\Lambda^{0}(\square_d)\) |
| Abbreviated names | S |
| Orders | \(1\leqslant k\) |
| Reference elements | interval, quadrilateral, hexahedron |
| Polynomial set | \(\mathcal{P}_{k} \oplus \mathcal{X}_{k}\)
↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑\(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|\sum_{i=1}^dp_i\leqslant k\right\}\)
\(\mathcal{X}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|k<\sum_{i=1}^da_i\leqslant k+\#\left\{i\in\{1,\dots,d\}\middle| a_i=1\right\}\right\}\) |
| DOFs | On each vertex: point evaluations
On each edge: integral moments with an order \(k-2\) dPc space
On each face: integral moments with an order \(k-4\) dPc space
On each volume: integral moments with an order \(k-6\) dPc space |
| Number of DOFs | interval: \(k+1\) (A000027)
quadrilateral: \(\begin{cases}4&k=1\\k(k+3)/2+3&k>1\end{cases}\) (A340266)
hexahedron: \(\begin{cases}12k-4&k=1,2,3\\3k^2-3k+14&k=4,5\\k(k-1)(k+1)/6+k^2+5k+4&k>6\end{cases}\) |
| Mapping | identity |
| continuity | Function values are continuous. |
| Categories | Scalar-valued elements |
| Basix | basix.ElementFamily.serendipity, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced
↓ Show Basix examples ↓↑ Hide Basix examples ↑Before trying this example, you must install Basix: pip3 install git+https://github.com/FEniCS/basix.git This element can then be created with the following lines of Python: import basix
# Create serendipity order 1 on a interval
element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 2 on a interval
element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 3 on a interval
element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 1 on a quadrilateral
element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 2 on a quadrilateral
element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 3 on a quadrilateral
element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) |
| Basix.UFL | basix.ElementFamily.serendipity, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced
↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑Before trying this example, you must install Basix.UFL: pip3 install git+https://github.com/FEniCS/basix.git git+https://github.com/FEniCS/ufl.git This element can then be created with the following lines of Python: import basix
import basix.ufl
# Create serendipity order 1 on a interval
element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 2 on a interval
element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 3 on a interval
element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 1 on a quadrilateral
element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 2 on a quadrilateral
element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced)
# Create serendipity order 3 on a quadrilateral
element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) |
| FIAT | FIAT.Serendipity
↓ Show FIAT examples ↓↑ Hide FIAT examples ↑Before trying this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT
# Create serendipity order 1
element = FIAT.Serendipity(FIAT.ufc_cell("interval"), 1)
# Create serendipity order 2
element = FIAT.Serendipity(FIAT.ufc_cell("interval"), 2)
# Create serendipity order 3
element = FIAT.Serendipity(FIAT.ufc_cell("interval"), 3)
# Create serendipity order 1
element = FIAT.Serendipity(FIAT.reference_element.UFCQuadrilateral(), 1)
# Create serendipity order 2
element = FIAT.Serendipity(FIAT.reference_element.UFCQuadrilateral(), 2)
# Create serendipity order 3
element = FIAT.Serendipity(FIAT.reference_element.UFCQuadrilateral(), 3) |
| Symfem | "serendipity"
↓ Show Symfem examples ↓↑ Hide Symfem examples ↑Before trying this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem
# Create serendipity order 1 on a interval
element = symfem.create_element("interval", "serendipity", 1)
# Create serendipity order 2 on a interval
element = symfem.create_element("interval", "serendipity", 2)
# Create serendipity order 3 on a interval
element = symfem.create_element("interval", "serendipity", 3)
# Create serendipity order 1 on a quadrilateral
element = symfem.create_element("quadrilateral", "serendipity", 1)
# Create serendipity order 2 on a quadrilateral
element = symfem.create_element("quadrilateral", "serendipity", 2)
# Create serendipity order 3 on a quadrilateral
element = symfem.create_element("quadrilateral", "serendipity", 3) |
| (legacy) UFL | "S"
↓ Show (legacy) UFL examples ↓↑ Hide (legacy) UFL examples ↑Before trying this example, you must install (legacy) UFL: pip3 install setuptools
pip3 install fenics-ufl-legacy
This element can then be created with the following lines of Python: import ufl_legacy
# Create serendipity order 1 on a interval
element = ufl_legacy.FiniteElement("S", "interval", 1)
# Create serendipity order 2 on a interval
element = ufl_legacy.FiniteElement("S", "interval", 2)
# Create serendipity order 3 on a interval
element = ufl_legacy.FiniteElement("S", "interval", 3)
# Create serendipity order 1 on a quadrilateral
element = ufl_legacy.FiniteElement("S", "quadrilateral", 1)
# Create serendipity order 2 on a quadrilateral
element = ufl_legacy.FiniteElement("S", "quadrilateral", 2)
# Create serendipity order 3 on a quadrilateral
element = ufl_legacy.FiniteElement("S", "quadrilateral", 3) |