Serendipity H(curl)
Click here to read what the information on this page means.
| Alternative names | Brezzi–Douglas–Marini cubical H(curl) (quadrilateral), Arnold–Awanou H(curl) (hexahedron) |
| De Rham complex families | \(\left[S_{1,k}^\square\right]_{1}\) / \(\mathcal{S}_{k}\Lambda^{1}(\square_d)\) |
| Abbreviated names | BDMce (quadrilateral), AAe (hexahedron) |
| Orders | \(1\leqslant k\) |
| Reference elements | quadrilateral, hexahedron |
| Polynomial set | \(\mathcal{P}_{k}^d \oplus \mathcal{Z}^{(26)}_{k}\) (quadrilateral) \(\mathcal{P}_{k}^d \oplus \mathcal{A}_{k-1} \oplus \mathcal{Z}^{(27)}_{k}\) (hexahedron) ↓ Show polynomial set definitions ↓ |
| DOFs | On each edge: tangent integral moments with an order \(k\) dPc space On each face: integral moments with an order \(k-2\) vector dPc space On each volume: integral moments with an order \(k-4\) vector dPc space |
| Number of DOFs | quadrilateral: \(k^2+3k+4\) (A014206) hexahedron: \(\begin{cases}6(k^2+k+2)&k=1,2,3\\k(k+1)(k-1)/2 + 3k^2 + 12k + 9&k > 3\end{cases}\) |
| Mapping | covariant Piola |
| continuity | Components tangential to facets are continuous |
| Categories | Vector-valued elements, H(curl) conforming elements |
Implementations
"Scurl"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. | |
"BDMCE" (quadrilateral)"AAE" (hexahedron)↓ Show (legacy) UFL examples ↓ |
Examples
| quadrilateral order 1 | 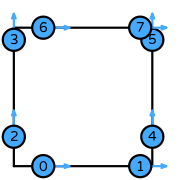 (click to view basis functions) |
| quadrilateral order 2 | 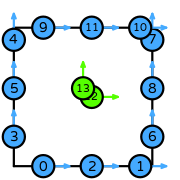 (click to view basis functions) |
| hexahedron order 1 | 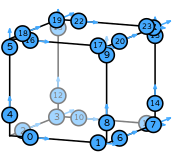 (click to view basis functions) |
| hexahedron order 2 | 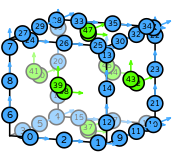 (click to view basis functions) |
References
- Arnold, Douglas N. and Awanou, Gerard. Finite element differential forms on cubical meshes, Mathematics of computation 83, 1551–5170, 2014. [DOI: 10.1090/S0025-5718-2013-02783-4] [BibTeX]
- Arnold, Douglas N. and Logg, Anders. Periodic table of the finite elements, SIAM News 47, 2014. [sinews.siam.org/Details-Page/periodic-table-of-the-finite-elements] [BibTeX]
- Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM journal on numerical analysis 55, 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]
DefElement stats
| Element added | 31 December 2020 |
| Element last updated | 16 September 2023 |