an encyclopedia of finite element definitions
Nonconforming Arnold–Winther
Click here to read what the information on this page means.
| Orders | \(k=2\) |
| Reference elements | triangle |
| Polynomial set | \(\mathcal{Z}^{(21)}_{k-1}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each edge: integral moments of normal-normal and normal-tangent inner products with an order \(1\) Lagrange space On each face: integral moments of three components with an order \(0\) Lagrange space |
| Number of DOFs | triangle: \(15\) |
| Categories | Matrix-valued elements |
Implementations
FIAT.ArnoldWintherNC↓ Show FIAT examples ↓ This implementation is correct for all the examples below. | |
"nonconforming AW"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. | |
"AWnc"↓ Show (legacy) UFL examples ↓ |
Examples
| triangle order 2 | 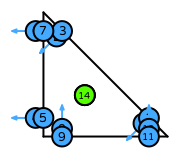 (click to view basis functions) |
References
- Arnold, Douglas N. and Winther, Ragnar. Nonconforming mixed elements for elasticity, Numerische Mathematik 13(3), 295–307, 2003. [DOI: 10.1142/S0218202503002507] [BibTeX]
DefElement stats
| Element added | 02 August 2021 |
| Element last updated | 16 September 2023 |