an encyclopedia of finite element definitions
Huang–Zhang
Click here to read what the information on this page means.
| Alternative names | \(Q_{k+1,k}\times Q_{k,k+1}\) |
| Abbreviated names | HZ |
| Orders | \(2\leqslant k\) |
| Reference elements | quadrilateral |
| Polynomial set | \(\mathcal{Z}^{(13)}_{k} \oplus \mathcal{Z}^{(14)}_{k}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each facet: normal integral moments with an order \(k-1\) Lagrange space, and tangent integral moments with an order \(k-2\) Lagrange space On the interior of the reference element: integral moments with \(\left\{\left(\begin{array}{c}x^iy^j\\0\end{array}\right)\middle|i\in\{0,1,...,k-1\}, j\in\{0,1,...,k-2\}\right\}\cup\left\{\left(\begin{array}{c}x^iy^j\\0\end{array}\right)\middle|i\in\{0,1,...,k-2\}, j\in\{0,1,...,k-1\}\right\}\) |
| Number of DOFs | quadrilateral: \(2k(k+1)\) (A046092) |
| Mapping | contravariant Piola |
| continuity | Components normal to facets are continuous |
| Categories | Vector-valued elements, H(div) conforming elements |
Implementations
"HZ"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| quadrilateral order 2 | 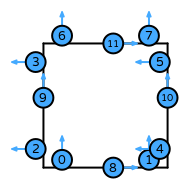 (click to view basis functions) |
| quadrilateral order 3 | 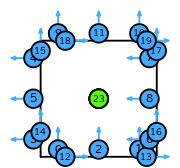 (click to view basis functions) |
References
- Zhang, Shangyou. A family of \(Q_{k+1,k}\times Q+{k,k+1}\) divergence-free finite elements on rectangular grids, SIAM journal on numerical analysis 47(3), 2090–2107, 2009. [DOI: 10.1137/080728949] [BibTeX]
- Huang, Yunqing and Zhang, Shangyou. A lowest order divergence-free finite element on rectangular grids, Frontiers of mathematics in China 6, 253–270, 2011. [DOI: 10.1007/s11464-011-0094-0] [BibTeX]
DefElement stats
| Element added | 09 December 2022 |
| Element last updated | 16 September 2023 |