an encyclopedia of finite element definitions
Hsieh–Clough–Tocher
Click here to read what the information on this page means.
| Alternative names | Clough–Tocher |
| De Rham complex families | \(\mathrm{C}^1\mathrm{P}^3\mathrm{\Lambda}^0(\mathcal{R})\) |
| Abbreviated names | HCT, CT |
| Degrees | \(3\leqslant k\) |
| Reference elements | triangle |
| DOFs | On each vertex: point evaluations, and point evaluations of first derivatives On each edge: normal derivative integral moments with an degree \(k-3\) Lagrange space, and integral moments with an degree \(k-4\) Lagrange space On each face: integral moments with an degree \(k-4\) Lagrange space |
| Number of DOFs | triangle: \(12+6(k-3)+(k-3)(k-2)/2\) |
| Mapping | identity |
| continuity | Function values and derivatives are continuous. |
| Categories | Scalar-valued elements, Macro elements |
Implementations
This element is implemented in FIAT and Symfem .↓ Show implementation detail ↓Examples
| triangle degree 3 | 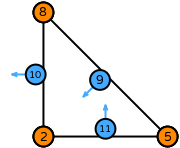 (click to view basis functions) |
References
- Clough, Ray W. and Tocher, James L. Finite element stiffness matrices for analysis of plate bending, Proceedings of the First Conference on Matrix Methods in Structural Mechanics, 515–546, 1965. [BibTeX]
- Ciarlet, Philippe G. Interpolation error estimates for the reduced Hsieh–Clough–Tocher triangle, Mathematics of Computation 32, 335–344, 1978. [DOI: 10.1090/S0025-5718-1978-0482249-1] [BibTeX]
- Grošelj, Jan and Knez, Marjeta. Generalized C1 Clough–Tocher splines for CAGD and FEM, Computer Methods in Applied Mechanics and Engineering 395, 2022. [DOI: 10.1016/j.cma.2022.114983] [BibTeX]
DefElement stats
| Element added | 08 March 2021 |
| Element last updated | 27 September 2024 |