Conforming Crouzeix–Raviart
Click here to read what the information on this page means.
| Abbreviated names | conforming CR |
| Orders | \(1\leqslant k\) |
| Reference elements | triangle |
| Polynomial set | \(\mathcal{P}_{k} \oplus \mathcal{Z}^{(12)}_{k}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each vertex: points evaluation On each edge: point evaluations On each face: point evaluations |
| Number of DOFs | triangle: \(k(k+5)/2\) |
| Mapping | identity |
| continuity | Discontinuous. |
| Categories | Scalar-valued elements |
Implementations
"conforming Crouzeix-Raviart"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| triangle order 1 | 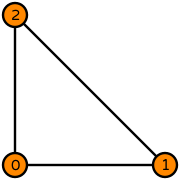 (click to view basis functions) |
| triangle order 2 | 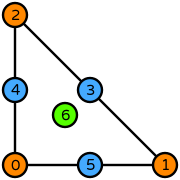 (click to view basis functions) |
| triangle order 3 | 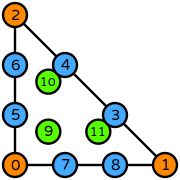 (click to view basis functions) |
| triangle order 4 | 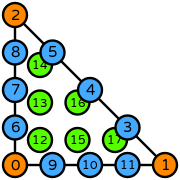 (click to view basis functions) |
| triangle order 5 |  (click to view basis functions) |
References
- Crouzeix, Michel and Raviart, Pierre-Arnaud. Conforming and nonconforming finite element methods for solving the stationary Stokes equations, Revue Française d'Automatique, Informatique et Recherche Opérationnelle 3, 33–75, 1973. [DOI: 10.1051/m2an/197307R300331] [BibTeX]
DefElement stats
| Element added | 04 July 2021 |
| Element last updated | 16 September 2023 |