an encyclopedia of finite element definitions
Degree 4 conforming Crouzeix–Raviart on a triangle
◀ Back to conforming Crouzeix–Raviart definition page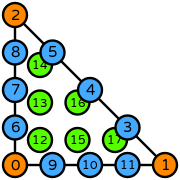
- \(R\) is the reference triangle. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(1\), \(x\), \(x^{2}\), \(x^{3}\), \(x^{4}\), \(y\), \(x y\), \(x^{2} y\), \(x^{3} y\), \(y^{2}\), \(x y^{2}\), \(x^{2} y^{2}\), \(y^{3}\), \(x y^{3}\), \(y^{4}\), \(x y^{3} \left(x + y\right)\), \(x^{2} y^{2} \left(x + y\right)\), \(x^{3} y \left(x + y\right)\)
- \(\mathcal{L}=\{l_0,...,l_{17}\}\)
- Functionals and basis functions:

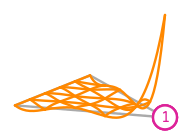
\(\displaystyle l_{0}:v\mapsto v(0,0)\)
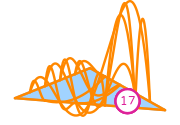
\(\displaystyle \phi_{0} = - \frac{208 x^{4} y}{5} + \frac{32 x^{4}}{3} - \frac{2896 x^{3} y^{2}}{25} + \frac{3316 x^{3} y}{25} - \frac{80 x^{3}}{3} - \frac{2896 x^{2} y^{3}}{25} + \frac{17624 x^{2} y^{2}}{75} - \frac{10676 x^{2} y}{75} + \frac{70 x^{2}}{3} - \frac{208 x y^{4}}{5} + \frac{3316 x y^{3}}{25} - \frac{10676 x y^{2}}{75} + \frac{1516 x y}{25} - \frac{25 x}{3} + \frac{32 y^{4}}{3} - \frac{80 y^{3}}{3} + \frac{70 y^{2}}{3} - \frac{25 y}{3} + 1\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \phi_{0} = - \frac{208 x^{4} y}{5} + \frac{32 x^{4}}{3} - \frac{2896 x^{3} y^{2}}{25} + \frac{3316 x^{3} y}{25} - \frac{80 x^{3}}{3} - \frac{2896 x^{2} y^{3}}{25} + \frac{17624 x^{2} y^{2}}{75} - \frac{10676 x^{2} y}{75} + \frac{70 x^{2}}{3} - \frac{208 x y^{4}}{5} + \frac{3316 x y^{3}}{25} - \frac{10676 x y^{2}}{75} + \frac{1516 x y}{25} - \frac{25 x}{3} + \frac{32 y^{4}}{3} - \frac{80 y^{3}}{3} + \frac{70 y^{2}}{3} - \frac{25 y}{3} + 1\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{1}:v\mapsto v(1,0)\)
\(\displaystyle \phi_{1} = \frac{x \left(- 3120 x^{3} y + 800 x^{3} - 3792 x^{2} y^{2} + 5732 x^{2} y - 1200 x^{2} - 1344 x y^{3} + 3956 x y^{2} - 3152 x y + 550 x - 672 y^{4} + 1344 y^{3} - 1212 y^{2} + 540 y - 75\right)}{75}\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \phi_{1} = \frac{x \left(- 3120 x^{3} y + 800 x^{3} - 3792 x^{2} y^{2} + 5732 x^{2} y - 1200 x^{2} - 1344 x y^{3} + 3956 x y^{2} - 3152 x y + 550 x - 672 y^{4} + 1344 y^{3} - 1212 y^{2} + 540 y - 75\right)}{75}\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{2}:v\mapsto v(0,1)\)
\(\displaystyle \phi_{2} = \frac{y \left(- 672 x^{4} - 1344 x^{3} y + 1344 x^{3} - 3792 x^{2} y^{2} + 3956 x^{2} y - 1212 x^{2} - 3120 x y^{3} + 5732 x y^{2} - 3152 x y + 540 x + 800 y^{3} - 1200 y^{2} + 550 y - 75\right)}{75}\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \phi_{2} = \frac{y \left(- 672 x^{4} - 1344 x^{3} y + 1344 x^{3} - 3792 x^{2} y^{2} + 3956 x^{2} y - 1212 x^{2} - 3120 x y^{3} + 5732 x y^{2} - 3152 x y + 540 x + 800 y^{3} - 1200 y^{2} + 550 y - 75\right)}{75}\)
This DOF is associated with vertex 2 of the reference element.
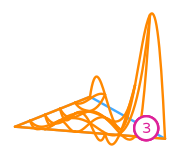
\(\displaystyle l_{3}:v\mapsto v(\tfrac{3}{4},\tfrac{1}{4})\)
\(\displaystyle \phi_{3} = \frac{16 x y \left(168 x^{3} + 120 x^{2} y - 230 x^{2} - 24 x y^{2} - 56 x y + 87 x + 24 y^{3} - 26 y^{2} + 17 y - 10\right)}{15}\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle \phi_{3} = \frac{16 x y \left(168 x^{3} + 120 x^{2} y - 230 x^{2} - 24 x y^{2} - 56 x y + 87 x + 24 y^{3} - 26 y^{2} + 17 y - 10\right)}{15}\)
This DOF is associated with edge 0 of the reference element.
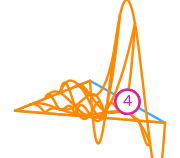
\(\displaystyle l_{4}:v\mapsto v(\tfrac{1}{2},\tfrac{1}{2})\)
\(\displaystyle \phi_{4} = \frac{2 x y \left(- 168 x^{3} + 456 x^{2} y + 134 x^{2} + 456 x y^{2} - 532 x y - x - 168 y^{3} + 134 y^{2} - y + 5\right)}{5}\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle \phi_{4} = \frac{2 x y \left(- 168 x^{3} + 456 x^{2} y + 134 x^{2} + 456 x y^{2} - 532 x y - x - 168 y^{3} + 134 y^{2} - y + 5\right)}{5}\)
This DOF is associated with edge 0 of the reference element.
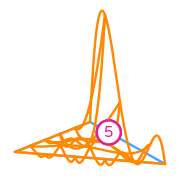
\(\displaystyle l_{5}:v\mapsto v(\tfrac{1}{4},\tfrac{3}{4})\)
\(\displaystyle \phi_{5} = \frac{16 x y \left(24 x^{3} - 24 x^{2} y - 26 x^{2} + 120 x y^{2} - 56 x y + 17 x + 168 y^{3} - 230 y^{2} + 87 y - 10\right)}{15}\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle \phi_{5} = \frac{16 x y \left(24 x^{3} - 24 x^{2} y - 26 x^{2} + 120 x y^{2} - 56 x y + 17 x + 168 y^{3} - 230 y^{2} + 87 y - 10\right)}{15}\)
This DOF is associated with edge 0 of the reference element.
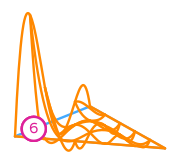
\(\displaystyle l_{6}:v\mapsto v(0,\tfrac{1}{4})\)
\(\displaystyle \phi_{6} = \frac{16 y \left(168 x^{4} + 552 x^{3} y - 442 x^{3} + 624 x^{2} y^{2} - 1022 x^{2} y + 405 x^{2} + 240 x y^{3} - 644 x y^{2} + 545 x y - 146 x - 40 y^{3} + 90 y^{2} - 65 y + 15\right)}{15}\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle \phi_{6} = \frac{16 y \left(168 x^{4} + 552 x^{3} y - 442 x^{3} + 624 x^{2} y^{2} - 1022 x^{2} y + 405 x^{2} + 240 x y^{3} - 644 x y^{2} + 545 x y - 146 x - 40 y^{3} + 90 y^{2} - 65 y + 15\right)}{15}\)
This DOF is associated with edge 1 of the reference element.
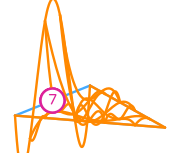
\(\displaystyle l_{7}:v\mapsto v(0,\tfrac{1}{2})\)
\(\displaystyle \phi_{7} = \frac{2 y \left(- 168 x^{4} - 1128 x^{3} y + 538 x^{3} - 1920 x^{2} y^{2} + 2450 x^{2} y - 607 x^{2} - 960 x y^{3} + 2240 x y^{2} - 1517 x y + 267 x + 160 y^{3} - 320 y^{2} + 190 y - 30\right)}{5}\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle \phi_{7} = \frac{2 y \left(- 168 x^{4} - 1128 x^{3} y + 538 x^{3} - 1920 x^{2} y^{2} + 2450 x^{2} y - 607 x^{2} - 960 x y^{3} + 2240 x y^{2} - 1517 x y + 267 x + 160 y^{3} - 320 y^{2} + 190 y - 30\right)}{5}\)
This DOF is associated with edge 1 of the reference element.
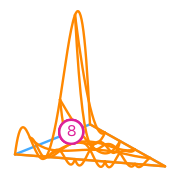
\(\displaystyle l_{8}:v\mapsto v(0,\tfrac{3}{4})\)
\(\displaystyle \phi_{8} = \frac{16 y \left(24 x^{4} + 120 x^{3} y - 70 x^{3} + 336 x^{2} y^{2} - 338 x^{2} y + 83 x^{2} + 240 x y^{3} - 476 x y^{2} + 263 x y - 42 x - 40 y^{3} + 70 y^{2} - 35 y + 5\right)}{15}\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle \phi_{8} = \frac{16 y \left(24 x^{4} + 120 x^{3} y - 70 x^{3} + 336 x^{2} y^{2} - 338 x^{2} y + 83 x^{2} + 240 x y^{3} - 476 x y^{2} + 263 x y - 42 x - 40 y^{3} + 70 y^{2} - 35 y + 5\right)}{15}\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{9}:v\mapsto v(\tfrac{1}{4},0)\)
\(\displaystyle \phi_{9} = \frac{16 x \left(240 x^{3} y - 40 x^{3} + 624 x^{2} y^{2} - 644 x^{2} y + 90 x^{2} + 552 x y^{3} - 1022 x y^{2} + 545 x y - 65 x + 168 y^{4} - 442 y^{3} + 405 y^{2} - 146 y + 15\right)}{15}\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle \phi_{9} = \frac{16 x \left(240 x^{3} y - 40 x^{3} + 624 x^{2} y^{2} - 644 x^{2} y + 90 x^{2} + 552 x y^{3} - 1022 x y^{2} + 545 x y - 65 x + 168 y^{4} - 442 y^{3} + 405 y^{2} - 146 y + 15\right)}{15}\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{10}:v\mapsto v(\tfrac{1}{2},0)\)
\(\displaystyle \phi_{10} = \frac{2 x \left(- 960 x^{3} y + 160 x^{3} - 1920 x^{2} y^{2} + 2240 x^{2} y - 320 x^{2} - 1128 x y^{3} + 2450 x y^{2} - 1517 x y + 190 x - 168 y^{4} + 538 y^{3} - 607 y^{2} + 267 y - 30\right)}{5}\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle \phi_{10} = \frac{2 x \left(- 960 x^{3} y + 160 x^{3} - 1920 x^{2} y^{2} + 2240 x^{2} y - 320 x^{2} - 1128 x y^{3} + 2450 x y^{2} - 1517 x y + 190 x - 168 y^{4} + 538 y^{3} - 607 y^{2} + 267 y - 30\right)}{5}\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{11}:v\mapsto v(\tfrac{3}{4},0)\)
\(\displaystyle \phi_{11} = \frac{16 x \left(240 x^{3} y - 40 x^{3} + 336 x^{2} y^{2} - 476 x^{2} y + 70 x^{2} + 120 x y^{3} - 338 x y^{2} + 263 x y - 35 x + 24 y^{4} - 70 y^{3} + 83 y^{2} - 42 y + 5\right)}{15}\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle \phi_{11} = \frac{16 x \left(240 x^{3} y - 40 x^{3} + 336 x^{2} y^{2} - 476 x^{2} y + 70 x^{2} + 120 x y^{3} - 338 x y^{2} + 263 x y - 35 x + 24 y^{4} - 70 y^{3} + 83 y^{2} - 42 y + 5\right)}{15}\)
This DOF is associated with edge 2 of the reference element.
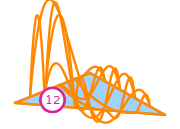
\(\displaystyle l_{12}:v\mapsto v(\tfrac{1}{6},\tfrac{1}{6})\)
\(\displaystyle \phi_{12} = 6 x y \left(- 72 x^{3} - 216 x^{2} y + 174 x^{2} - 216 x y^{2} + 348 x y - 137 x - 72 y^{3} + 174 y^{2} - 137 y + 35\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle \phi_{12} = 6 x y \left(- 72 x^{3} - 216 x^{2} y + 174 x^{2} - 216 x y^{2} + 348 x y - 137 x - 72 y^{3} + 174 y^{2} - 137 y + 35\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{13}:v\mapsto v(\tfrac{1}{6},\tfrac{5}{12})\)
\(\displaystyle \phi_{13} = \frac{384 x y \left(36 x^{2} y - 6 x^{2} + 72 x y^{2} - 78 x y + 11 x + 36 y^{3} - 72 y^{2} + 41 y - 5\right)}{25}\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle \phi_{13} = \frac{384 x y \left(36 x^{2} y - 6 x^{2} + 72 x y^{2} - 78 x y + 11 x + 36 y^{3} - 72 y^{2} + 41 y - 5\right)}{25}\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{14}:v\mapsto v(\tfrac{1}{6},\tfrac{2}{3})\)
\(\displaystyle \phi_{14} = 6 x y \left(- 72 x y^{2} + 42 x y - 5 x - 72 y^{3} + 114 y^{2} - 47 y + 5\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle \phi_{14} = 6 x y \left(- 72 x y^{2} + 42 x y - 5 x - 72 y^{3} + 114 y^{2} - 47 y + 5\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{15}:v\mapsto v(\tfrac{5}{12},\tfrac{1}{6})\)
\(\displaystyle \phi_{15} = \frac{384 x y \left(36 x^{3} + 72 x^{2} y - 72 x^{2} + 36 x y^{2} - 78 x y + 41 x - 6 y^{2} + 11 y - 5\right)}{25}\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle \phi_{15} = \frac{384 x y \left(36 x^{3} + 72 x^{2} y - 72 x^{2} + 36 x y^{2} - 78 x y + 41 x - 6 y^{2} + 11 y - 5\right)}{25}\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{16}:v\mapsto v(\tfrac{5}{12},\tfrac{5}{12})\)
\(\displaystyle \phi_{16} = \frac{384 x y \left(- 36 x^{2} y + 6 x^{2} - 36 x y^{2} + 48 x y - 7 x + 6 y^{2} - 7 y + 1\right)}{25}\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle \phi_{16} = \frac{384 x y \left(- 36 x^{2} y + 6 x^{2} - 36 x y^{2} + 48 x y - 7 x + 6 y^{2} - 7 y + 1\right)}{25}\)
This DOF is associated with face 0 of the reference element.