an encyclopedia of finite element definitions

Vector Q

Click here to read what the information on this page means.

Alternative names	vector Lagrange
Degrees	\(0\leqslant k\) where \(k\) is the Lagrange superdegree
Polynomial subdegree	\(k\)
Polynomial superdegree	\(dk\)
Lagrange subdegree	\(k\)
Lagrange superdegree	\(k\)
Reference elements	quadrilateral, hexahedron
Polynomial set	\(\mathcal{Q}_{k}^d\) ↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑ \(\mathcal{Q}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\max_i(p_i)\leqslant k\right\}\)
DOFs	On each vertex: point evaluations in coordinate directions On each edge: point evaluations in coordinate directions On each face: point evaluations in coordinate directions On each volume: point evaluations in coordinate directions
Number of DOFs	interval: \(k+1\) (A000027) quadrilateral: \(2(k+1)^2\) (A001105) hexahedron: \(3(k+1)^3\) (A117642)
Mapping	identity
continuity	Function values are continuous.
Categories	Vector-valued elements

Implementations

This element is implemented in Basix.UFL , Symfem , and (legacy) UFL.↓ Show implementation detail ↓

↑ Hide implementation detail ↑

Basix.UFL	`basix.ElementFamily.P, lagrange_variant=basix.LagrangeVariant.equispaced, shape=(dim,)` ↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑ Before running this example, you must install Basix.UFL: pip3 install fenics-basix fenics-ufl This element can then be created with the following lines of Python: import basix import basix.ufl # Create vector Q degree 1 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced, shape=(2,)) # Create vector Q degree 2 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced, shape=(2,)) # Create vector Q degree 1 on a hexahedron element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.hexahedron, 1, lagrange_variant=basix.LagrangeVariant.equispaced, shape=(3,)) # Create vector Q degree 2 on a hexahedron element = basix.ufl.element(basix.ElementFamily.P, basix.CellType.hexahedron, 2, lagrange_variant=basix.LagrangeVariant.equispaced, shape=(3,)) This implementation is correct for all the examples below.
Symfem	`"vector Q"` ↓ Show Symfem examples ↓↑ Hide Symfem examples ↑ Before running this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem # Create vector Q degree 1 on a quadrilateral element = symfem.create_element("quadrilateral", "vector Q", 1) # Create vector Q degree 2 on a quadrilateral element = symfem.create_element("quadrilateral", "vector Q", 2) # Create vector Q degree 1 on a hexahedron element = symfem.create_element("hexahedron", "vector Q", 1) # Create vector Q degree 2 on a hexahedron element = symfem.create_element("hexahedron", "vector Q", 2) This implementation is used to compute the examples below and verify other implementations.
(legacy) UFL	`"Q"` ↓ Show (legacy) UFL examples ↓↑ Hide (legacy) UFL examples ↑ Before running this example, you must install (legacy) UFL: pip3 install setuptools pip3 install fenics-ufl-legacy This element can then be created with the following lines of Python: import ufl_legacy # Create vector Q degree 1 on a quadrilateral element = ufl_legacy.VectorElement("Q", "quadrilateral", 1) # Create vector Q degree 2 on a quadrilateral element = ufl_legacy.VectorElement("Q", "quadrilateral", 2) # Create vector Q degree 1 on a hexahedron element = ufl_legacy.VectorElement("Q", "hexahedron", 1) # Create vector Q degree 2 on a hexahedron element = ufl_legacy.VectorElement("Q", "hexahedron", 2)

Examples

quadrilateral degree 1	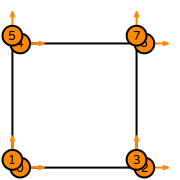(click to view basis functions)
quadrilateral degree 2	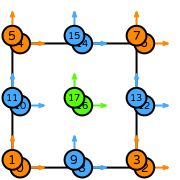(click to view basis functions)
hexahedron degree 1	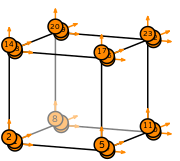(click to view basis functions)
hexahedron degree 2	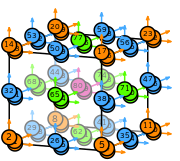(click to view basis functions)

DefElement stats

Element added	30 December 2020
Element last updated	27 September 2024