an encyclopedia of finite element definitions
Kong–Mulder–Veldhuizen
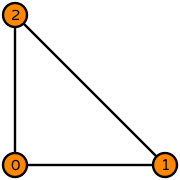
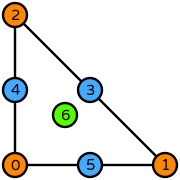
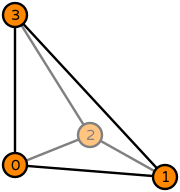
Click here to read what the information on this page means.
| Abbreviated names | KMV |
| Orders | \(0\leqslant k\) |
| Reference elements | triangle, tetrahedron |
| Categories | Scalar-valued elements |
Implementations
"KMV"↓ Show Symfem examples ↓ | |
"KMV"↓ Show UFL examples ↓ |
Examples
triangleorder 1triangle
order 3tetrahedron
order 1
- \(R\) is the reference triangle. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(1\), \(x\), \(y\)
- \(\mathcal{L}=\{l_0,...,l_{2}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:v\mapsto \frac{1}{6} v(0,0)\)
\(\displaystyle \phi_{0} = - 6 x - 6 y + 6\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \phi_{0} = - 6 x - 6 y + 6\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{1}:v\mapsto \frac{1}{6} v(1,0)\)
\(\displaystyle \phi_{1} = 6 x\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \phi_{1} = 6 x\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{2}:v\mapsto \frac{1}{6} v(0,1)\)
\(\displaystyle \phi_{2} = 6 y\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \phi_{2} = 6 y\)
This DOF is associated with vertex 2 of the reference element.
- \(R\) is the reference triangle. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(1\), \(x\), \(x^{2}\), \(y\), \(x y\), \(y^{2}\), \(x y \left(- x - y + 1\right)\)
- \(\mathcal{L}=\{l_0,...,l_{6}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:v\mapsto \frac{1}{40} v(0,0)\)
\(\displaystyle \phi_{0} = - 120 x^{2} y + 80 x^{2} - 120 x y^{2} + 280 x y - 120 x + 80 y^{2} - 120 y + 40\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \phi_{0} = - 120 x^{2} y + 80 x^{2} - 120 x y^{2} + 280 x y - 120 x + 80 y^{2} - 120 y + 40\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{1}:v\mapsto \frac{1}{40} v(1,0)\)
\(\displaystyle \phi_{1} = 40 x \left(- 3 x y + 2 x - 3 y^{2} + 3 y - 1\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \phi_{1} = 40 x \left(- 3 x y + 2 x - 3 y^{2} + 3 y - 1\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{2}:v\mapsto \frac{1}{40} v(0,1)\)
\(\displaystyle \phi_{2} = 40 y \left(- 3 x^{2} - 3 x y + 3 x + 2 y - 1\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \phi_{2} = 40 y \left(- 3 x^{2} - 3 x y + 3 x + 2 y - 1\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle l_{3}:v\mapsto \frac{1}{15} v(\tfrac{1}{2},\tfrac{1}{2})\)
\(\displaystyle \phi_{3} = 60 x y \left(3 x + 3 y - 2\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle \phi_{3} = 60 x y \left(3 x + 3 y - 2\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{4}:v\mapsto \frac{1}{15} v(0,\tfrac{1}{2})\)
\(\displaystyle \phi_{4} = 60 y \left(3 x^{2} + 3 x y - 4 x - y + 1\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle \phi_{4} = 60 y \left(3 x^{2} + 3 x y - 4 x - y + 1\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{5}:v\mapsto \frac{1}{15} v(\tfrac{1}{2},0)\)
\(\displaystyle \phi_{5} = 60 x \left(3 x y - x + 3 y^{2} - 4 y + 1\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle \phi_{5} = 60 x \left(3 x y - x + 3 y^{2} - 4 y + 1\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{6}:v\mapsto \frac{9}{40} v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{6} = 120 x y \left(- x - y + 1\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle \phi_{6} = 120 x y \left(- x - y + 1\right)\)
This DOF is associated with face 0 of the reference element.
- \(R\) is the reference tetrahedron. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(1\), \(x\), \(y\), \(z\)
- \(\mathcal{L}=\{l_0,...,l_{3}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:v\mapsto \frac{1}{24} v(0,0,0)\)
\(\displaystyle \phi_{0} = - 24 x - 24 y - 24 z + 24\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \phi_{0} = - 24 x - 24 y - 24 z + 24\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{1}:v\mapsto \frac{1}{24} v(1,0,0)\)
\(\displaystyle \phi_{1} = 24 x\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \phi_{1} = 24 x\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{2}:v\mapsto \frac{1}{24} v(0,1,0)\)
\(\displaystyle \phi_{2} = 24 y\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \phi_{2} = 24 y\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle l_{3}:v\mapsto \frac{1}{24} v(0,0,1)\)
\(\displaystyle \phi_{3} = 24 z\)
This DOF is associated with vertex 3 of the reference element.
\(\displaystyle \phi_{3} = 24 z\)
This DOF is associated with vertex 3 of the reference element.
References
- Chin-Joe-Kong, M. J. S., Mulder, Wim A., and Van Veldhuizen, M. Higher-order triangular and tetrahedral finite elements with mass lumping for solving the wave equation, Journal of Engineering Mathematics 35, 405–426, 1999. [DOI: 10.1023/A:1004420829610] [BibTeX]
DefElement stats
| Element added | 09 May 2021 |
| Element last updated | 10 February 2022 |