an encyclopedia of finite element definitions
Fortin–Soulie
Click here to read what the information on this page means.
| Abbreviated names | FS |
| Orders | \(k=2\) |
| Reference elements | triangle |
| Polynomial set | \(\mathcal{P}_{k}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each facet: point evaluation at two points (but only one point on one of the edges) On the interior of the reference element: point evaluation at midpoint |
| Number of DOFs | triangle: \(6\) |
| Mapping | identity |
| continuity | Discontinuous. |
| Categories | Scalar-valued elements |
Implementations
"Fortin-Soulie"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| triangle order 2 | 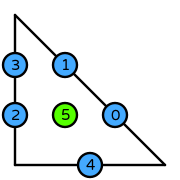 (click to view basis functions) |
References
- Fortin, Michel and Soulie, M. A non‐conforming piecewise quadratic finite element on triangles, International Journal for Numerical Methods in Engineering 19, 505–520, 1983. [DOI: 10.1002/nme.1620190405] [BibTeX]
DefElement stats
| Element added | 06 March 2021 |
| Element last updated | 16 September 2023 |