Direct serendipity
Click here to read what the information on this page means.
| Orders | \(1\leqslant k\) |
| Reference elements | quadrilateral |
| Mapping | identity |
| continuity | Function values are continuous. |
| Categories | Scalar-valued elements |
Implementations
"direct serendipity"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. | |
"Sdirect"↓ Show (legacy) UFL examples ↓ |
Examples
| quadrilateral order 1 | 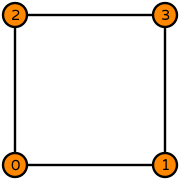 (click to view basis functions) |
| quadrilateral order 2 | 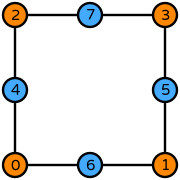 (click to view basis functions) |
| quadrilateral order 3 | 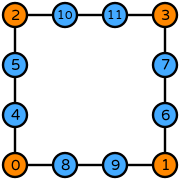 (click to view basis functions) |
References
- Arbogast, Todd and Tao, Zhong. Direct serendipity and mixed finite elements on convex quadrilaterals, arΧiv: 1809.02192, 2018. [BibTeX]
DefElement stats
| Element added | 27 May 2021 |
| Element last updated | 16 September 2023 |