an encyclopedia of finite element definitions
Bogner–Fox–Schmitt
Click here to read what the information on this page means.
| Orders | \(k=3\) |
| Reference elements | quadrilateral |
| Polynomial set | \(\mathcal{Q}_{k}\) ↓ Show polynomial set definitions ↓ |
| DOFs | On each vertex: point evaluations, point evaluations of derivatives in coordinate directions, and point evaluation of mixed second derivative |
| Number of DOFs | quadrilateral: \(16\) |
| Mapping | identity |
| continuity | Function values and derivatives are continuous. |
| Categories | Scalar-valued elements |
Implementations
"BFS"↓ Show Symfem examples ↓ This implementation is used to compute the examples below and verify other implementations. |
Examples
| quadrilateral order 3 | 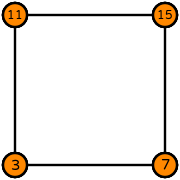 (click to view basis functions) |
References
- Bogner, F. K., Fox, R. L., and Schmit, L. A. The generation of interelement compatible stiffness and mass matrices by the use of interpolation formulae, Proceedings of the Conference on Matrix Methods in Structural Mechanics, 397–444, 1965. [BibTeX]
DefElement stats
| Element added | 06 March 2021 |
| Element last updated | 16 September 2023 |