an encyclopedia of finite element definitions

Bernstein

Click here to read what the information on this page means.

Alternative names	Bernstein–Bézier
Degrees	\(0\leqslant k\) where \(k\) is the Polynomial superdegree
Polynomial subdegree	\(k\)
Polynomial superdegree	\(k\)
Reference elements	interval, triangle, tetrahedron
Polynomial set	\(\mathcal{P}_{k}\) ↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑ \(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\sum_{i=1}^dp_i\leqslant k\right\}\)
DOFs	On each vertex: point evaluations On each edge: evaluation of Bernstein coefficients On each face: evaluation of Bernstein coefficients On each volume: evaluation of Bernstein coefficients
Number of DOFs	interval: \(k+1\) (A000027) triangle: \((k+1)(k+2)/2\) (A000217) tetrahedron: \((k+1)(k+2)(k+3)/6\) (A000292)
Mapping	identity
continuity	Function values are continuous.
Categories	Scalar-valued elements

Implementations

This element is implemented in FIAT , Symfem , and (legacy) UFL.↓ Show implementation detail ↓

↑ Hide implementation detail ↑

FIAT	`FIAT.Bernstein` ↓ Show FIAT examples ↓↑ Hide FIAT examples ↑ Before running this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT # Create Bernstein degree 1 element = FIAT.Bernstein(FIAT.ufc_cell("interval"), 1) # Create Bernstein degree 2 element = FIAT.Bernstein(FIAT.ufc_cell("interval"), 2) # Create Bernstein degree 3 element = FIAT.Bernstein(FIAT.ufc_cell("interval"), 3) # Create Bernstein degree 1 element = FIAT.Bernstein(FIAT.ufc_cell("triangle"), 1) # Create Bernstein degree 2 element = FIAT.Bernstein(FIAT.ufc_cell("triangle"), 2) # Create Bernstein degree 3 element = FIAT.Bernstein(FIAT.ufc_cell("triangle"), 3) This implementation is correct for all the examples below.
Symfem	`"Bernstein"` ↓ Show Symfem examples ↓↑ Hide Symfem examples ↑ Before running this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem # Create Bernstein degree 1 on a interval element = symfem.create_element("interval", "Bernstein", 1) # Create Bernstein degree 2 on a interval element = symfem.create_element("interval", "Bernstein", 2) # Create Bernstein degree 3 on a interval element = symfem.create_element("interval", "Bernstein", 3) # Create Bernstein degree 1 on a triangle element = symfem.create_element("triangle", "Bernstein", 1) # Create Bernstein degree 2 on a triangle element = symfem.create_element("triangle", "Bernstein", 2) # Create Bernstein degree 3 on a triangle element = symfem.create_element("triangle", "Bernstein", 3) This implementation is used to compute the examples below and verify other implementations.
(legacy) UFL	`"Bernstein"` ↓ Show (legacy) UFL examples ↓↑ Hide (legacy) UFL examples ↑ Before running this example, you must install (legacy) UFL: pip3 install setuptools pip3 install fenics-ufl-legacy This element can then be created with the following lines of Python: import ufl_legacy # Create Bernstein degree 1 on a interval element = ufl_legacy.FiniteElement("Bernstein", "interval", 1) # Create Bernstein degree 2 on a interval element = ufl_legacy.FiniteElement("Bernstein", "interval", 2) # Create Bernstein degree 3 on a interval element = ufl_legacy.FiniteElement("Bernstein", "interval", 3) # Create Bernstein degree 1 on a triangle element = ufl_legacy.FiniteElement("Bernstein", "triangle", 1) # Create Bernstein degree 2 on a triangle element = ufl_legacy.FiniteElement("Bernstein", "triangle", 2) # Create Bernstein degree 3 on a triangle element = ufl_legacy.FiniteElement("Bernstein", "triangle", 3)

Examples

interval degree 1	(click to view basis functions)
interval degree 2	(click to view basis functions)
interval degree 3	(click to view basis functions)
triangle degree 1	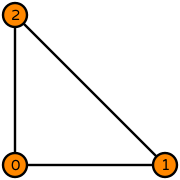(click to view basis functions)
triangle degree 2	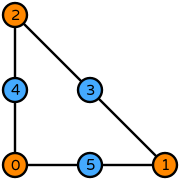(click to view basis functions)
triangle degree 3	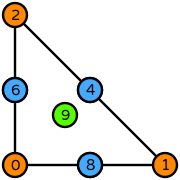(click to view basis functions)

References

Ainsworth, Mark, Andriamaro, Gaelle, and Davydov, Oleg. Bernstein–Bézier finite elements of arbitrary order and optimal assembly procedures, SIAM Journal on Scientific Computing 33(6), 3087–3109, 2011. [DOI: 10.1137/11082539X] [BibTeX]
Kirby, Robert C. Fast simplicial finite element algorithms using Bernstein polynomials, Numerische Mathematik 117(4), 631–652, 2011. [DOI: 10.1007/s00211-010-0327-2] [BibTeX]

DefElement stats

Element added	20 February 2021
Element last updated	27 September 2024