an encyclopedia of finite element definitions
Degree 4 Arnold–Winther on a triangle
◀ Back to Arnold–Winther definition page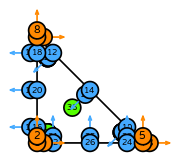
- \(R\) is the reference triangle. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(\left(\begin{array}{cc}\displaystyle 1&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 1\\\displaystyle 1&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 1\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle x&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x\\\displaystyle x&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle x^{2}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x^{2}\\\displaystyle x^{2}&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x^{2}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle x^{3}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x^{3}\\\displaystyle x^{3}&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x^{3}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle y&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle y\\\displaystyle y&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle y\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle x y&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x y\\\displaystyle x y&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x y\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle x^{2} y&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x^{2} y\\\displaystyle x^{2} y&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x^{2} y\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle y^{2}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle y^{2}\\\displaystyle y^{2}&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle y^{2}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle x y^{2}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x y^{2}\\\displaystyle x y^{2}&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x y^{2}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle y^{3}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle y^{3}\\\displaystyle y^{3}&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle y^{3}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 30 y^{4}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 20 x y^{3}&\displaystyle - 5 y^{4}\\\displaystyle - 5 y^{4}&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 12 x^{2} y^{2}&\displaystyle - 8 x y^{3}\\\displaystyle - 8 x y^{3}&\displaystyle - 2 y^{4}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 6 x^{3} y&\displaystyle - 9 x^{2} y^{2}\\\displaystyle - 9 x^{2} y^{2}&\displaystyle - 6 x y^{3}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 2 x^{4}&\displaystyle - 8 x^{3} y\\\displaystyle - 8 x^{3} y&\displaystyle - 12 x^{2} y^{2}\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle x^{4}\\\displaystyle x^{4}&\displaystyle - 4 x^{3} y\end{array}\right)\), \(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x^{4}\end{array}\right)\)
- \(\mathcal{L}=\{l_0,...,l_{36}\}\)
- Functionals and basis functions:

\(\displaystyle l_{0}:\mathbf{V}\mapsto\left(\begin{array}{c}1\\0\end{array}\right)^{\text{t}}\mathbf{V}(0,0)\left(\begin{array}{c}1\\0\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{0} = \left(\begin{array}{cc}\displaystyle 7 x^{4} + 140 x^{3} y - 28 x^{3} + 168 x^{2} y^{2} - 156 x^{2} y + 20 x^{2} + 35 y^{4} - 80 y^{3} + 60 y^{2} - 16 y + 1&\displaystyle 2 x y \left(- 14 x^{2} - 105 x y + 42 x - 56 y^{2} + 78 y - 20\right)\\\displaystyle 2 x y \left(- 14 x^{2} - 105 x y + 42 x - 56 y^{2} + 78 y - 20\right)&\displaystyle 2 y \left(- 21 x^{2} y + 12 x^{2} - 70 x y^{2} + 102 x y - 28 x - 14 y^{3} + 42 y^{2} - 36 y + 8\right)\end{array}\right)\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \mathbf{\Phi}_{0} = \left(\begin{array}{cc}\displaystyle 7 x^{4} + 140 x^{3} y - 28 x^{3} + 168 x^{2} y^{2} - 156 x^{2} y + 20 x^{2} + 35 y^{4} - 80 y^{3} + 60 y^{2} - 16 y + 1&\displaystyle 2 x y \left(- 14 x^{2} - 105 x y + 42 x - 56 y^{2} + 78 y - 20\right)\\\displaystyle 2 x y \left(- 14 x^{2} - 105 x y + 42 x - 56 y^{2} + 78 y - 20\right)&\displaystyle 2 y \left(- 21 x^{2} y + 12 x^{2} - 70 x y^{2} + 102 x y - 28 x - 14 y^{3} + 42 y^{2} - 36 y + 8\right)\end{array}\right)\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{1}:\mathbf{V}\mapsto\left(\begin{array}{c}1\\0\end{array}\right)^{\text{t}}\mathbf{V}(0,0)\left(\begin{array}{c}0\\1\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{1} = \left(\begin{array}{cc}\displaystyle 2 x \left(21 x^{3} - 14 x^{2} - 126 x y^{2} + 102 x y - 15 x - 70 y^{3} + 120 y^{2} - 60 y + 8\right)&\displaystyle 35 x^{4} - 168 x^{3} y - 80 x^{3} + 84 x^{2} y + 60 x^{2} + 168 x y^{3} - 204 x y^{2} + 60 x y - 16 x + 35 y^{4} - 80 y^{3} + 60 y^{2} - 16 y + 1\\\displaystyle 35 x^{4} - 168 x^{3} y - 80 x^{3} + 84 x^{2} y + 60 x^{2} + 168 x y^{3} - 204 x y^{2} + 60 x y - 16 x + 35 y^{4} - 80 y^{3} + 60 y^{2} - 16 y + 1&\displaystyle 2 y \left(- 70 x^{3} - 126 x^{2} y + 192 x^{2} + 102 x y - 108 x + 21 y^{3} - 38 y^{2} + 9 y + 8\right)\end{array}\right)\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \mathbf{\Phi}_{1} = \left(\begin{array}{cc}\displaystyle 2 x \left(21 x^{3} - 14 x^{2} - 126 x y^{2} + 102 x y - 15 x - 70 y^{3} + 120 y^{2} - 60 y + 8\right)&\displaystyle 35 x^{4} - 168 x^{3} y - 80 x^{3} + 84 x^{2} y + 60 x^{2} + 168 x y^{3} - 204 x y^{2} + 60 x y - 16 x + 35 y^{4} - 80 y^{3} + 60 y^{2} - 16 y + 1\\\displaystyle 35 x^{4} - 168 x^{3} y - 80 x^{3} + 84 x^{2} y + 60 x^{2} + 168 x y^{3} - 204 x y^{2} + 60 x y - 16 x + 35 y^{4} - 80 y^{3} + 60 y^{2} - 16 y + 1&\displaystyle 2 y \left(- 70 x^{3} - 126 x^{2} y + 192 x^{2} + 102 x y - 108 x + 21 y^{3} - 38 y^{2} + 9 y + 8\right)\end{array}\right)\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{2}:\mathbf{V}\mapsto\left(\begin{array}{c}0\\1\end{array}\right)^{\text{t}}\mathbf{V}(0,0)\left(\begin{array}{c}0\\1\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{2} = \left(\begin{array}{cc}\displaystyle x^{2} \left(- 140 x y + 20 x - 210 y^{2} + 180 y - 20\right)&\displaystyle 10 x y \left(21 x y - 6 x + 14 y^{2} - 18 y + 4\right)\\\displaystyle 10 x y \left(21 x y - 6 x + 14 y^{2} - 18 y + 4\right)&\displaystyle 35 x^{4} - 80 x^{3} + 60 x^{2} + 140 x y^{3} - 180 x y^{2} + 40 x y - 16 x + 35 y^{4} - 100 y^{3} + 80 y^{2} - 16 y + 1\end{array}\right)\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \mathbf{\Phi}_{2} = \left(\begin{array}{cc}\displaystyle x^{2} \left(- 140 x y + 20 x - 210 y^{2} + 180 y - 20\right)&\displaystyle 10 x y \left(21 x y - 6 x + 14 y^{2} - 18 y + 4\right)\\\displaystyle 10 x y \left(21 x y - 6 x + 14 y^{2} - 18 y + 4\right)&\displaystyle 35 x^{4} - 80 x^{3} + 60 x^{2} + 140 x y^{3} - 180 x y^{2} + 40 x y - 16 x + 35 y^{4} - 100 y^{3} + 80 y^{2} - 16 y + 1\end{array}\right)\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{3}:\mathbf{V}\mapsto\left(\begin{array}{c}1\\0\end{array}\right)^{\text{t}}\mathbf{V}(1,0)\left(\begin{array}{c}1\\0\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{3} = \left(\begin{array}{cc}\displaystyle x^{2} \left(- 7 x^{2} - 140 x y + 28 x - 168 y^{2} + 156 y - 20\right)&\displaystyle 2 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)\\\displaystyle 2 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)&\displaystyle 2 y \left(21 x^{2} y - 12 x^{2} + 70 x y^{2} - 102 x y + 28 x + 14 y^{3} - 42 y^{2} + 36 y - 8\right)\end{array}\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \mathbf{\Phi}_{3} = \left(\begin{array}{cc}\displaystyle x^{2} \left(- 7 x^{2} - 140 x y + 28 x - 168 y^{2} + 156 y - 20\right)&\displaystyle 2 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)\\\displaystyle 2 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)&\displaystyle 2 y \left(21 x^{2} y - 12 x^{2} + 70 x y^{2} - 102 x y + 28 x + 14 y^{3} - 42 y^{2} + 36 y - 8\right)\end{array}\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{4}:\mathbf{V}\mapsto\left(\begin{array}{c}1\\0\end{array}\right)^{\text{t}}\mathbf{V}(1,0)\left(\begin{array}{c}0\\1\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{4} = \left(\begin{array}{cc}\displaystyle x^{2} \left(- 560 x y + 80 x - 840 y^{2} + 720 y - 80\right)&\displaystyle x \left(35 x^{3} - 60 x^{2} + 840 x y^{2} - 240 x y + 30 x + 560 y^{3} - 720 y^{2} + 160 y - 4\right)\\\displaystyle x \left(35 x^{3} - 60 x^{2} + 840 x y^{2} - 240 x y + 30 x + 560 y^{3} - 720 y^{2} + 160 y - 4\right)&\displaystyle 20 y \left(- 7 x^{3} + 9 x^{2} + 28 x y^{2} - 36 x y + 5 x + 7 y^{3} - 20 y^{2} + 16 y - 3\right)\end{array}\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \mathbf{\Phi}_{4} = \left(\begin{array}{cc}\displaystyle x^{2} \left(- 560 x y + 80 x - 840 y^{2} + 720 y - 80\right)&\displaystyle x \left(35 x^{3} - 60 x^{2} + 840 x y^{2} - 240 x y + 30 x + 560 y^{3} - 720 y^{2} + 160 y - 4\right)\\\displaystyle x \left(35 x^{3} - 60 x^{2} + 840 x y^{2} - 240 x y + 30 x + 560 y^{3} - 720 y^{2} + 160 y - 4\right)&\displaystyle 20 y \left(- 7 x^{3} + 9 x^{2} + 28 x y^{2} - 36 x y + 5 x + 7 y^{3} - 20 y^{2} + 16 y - 3\right)\end{array}\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{5}:\mathbf{V}\mapsto\left(\begin{array}{c}0\\1\end{array}\right)^{\text{t}}\mathbf{V}(1,0)\left(\begin{array}{c}0\\1\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{5} = \left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x \left(35 x^{3} - 60 x^{2} + 30 x - 4\right)\end{array}\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \mathbf{\Phi}_{5} = \left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x \left(35 x^{3} - 60 x^{2} + 30 x - 4\right)\end{array}\right)\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{6}:\mathbf{V}\mapsto\left(\begin{array}{c}1\\0\end{array}\right)^{\text{t}}\mathbf{V}(0,1)\left(\begin{array}{c}1\\0\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{6} = \left(\begin{array}{cc}\displaystyle y \left(35 y^{3} - 60 y^{2} + 30 y - 4\right)&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \mathbf{\Phi}_{6} = \left(\begin{array}{cc}\displaystyle y \left(35 y^{3} - 60 y^{2} + 30 y - 4\right)&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle l_{7}:\mathbf{V}\mapsto\left(\begin{array}{c}1\\0\end{array}\right)^{\text{t}}\mathbf{V}(0,1)\left(\begin{array}{c}0\\1\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{7} = \left(\begin{array}{cc}\displaystyle 4 x \left(7 x^{3} + 140 x^{2} y - 28 x^{2} + 168 x y^{2} - 156 x y + 20 x - 35 y^{3} + 45 y^{2} - 15 y + 1\right)&\displaystyle y \left(- 112 x^{3} - 840 x^{2} y + 336 x^{2} - 448 x y^{2} + 624 x y - 160 x + 35 y^{3} - 60 y^{2} + 30 y - 4\right)\\\displaystyle y \left(- 112 x^{3} - 840 x^{2} y + 336 x^{2} - 448 x y^{2} + 624 x y - 160 x + 35 y^{3} - 60 y^{2} + 30 y - 4\right)&\displaystyle 8 y \left(- 21 x^{2} y + 12 x^{2} - 70 x y^{2} + 102 x y - 28 x - 14 y^{3} + 42 y^{2} - 36 y + 8\right)\end{array}\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \mathbf{\Phi}_{7} = \left(\begin{array}{cc}\displaystyle 4 x \left(7 x^{3} + 140 x^{2} y - 28 x^{2} + 168 x y^{2} - 156 x y + 20 x - 35 y^{3} + 45 y^{2} - 15 y + 1\right)&\displaystyle y \left(- 112 x^{3} - 840 x^{2} y + 336 x^{2} - 448 x y^{2} + 624 x y - 160 x + 35 y^{3} - 60 y^{2} + 30 y - 4\right)\\\displaystyle y \left(- 112 x^{3} - 840 x^{2} y + 336 x^{2} - 448 x y^{2} + 624 x y - 160 x + 35 y^{3} - 60 y^{2} + 30 y - 4\right)&\displaystyle 8 y \left(- 21 x^{2} y + 12 x^{2} - 70 x y^{2} + 102 x y - 28 x - 14 y^{3} + 42 y^{2} - 36 y + 8\right)\end{array}\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle l_{8}:\mathbf{V}\mapsto\left(\begin{array}{c}0\\1\end{array}\right)^{\text{t}}\mathbf{V}(0,1)\left(\begin{array}{c}0\\1\end{array}\right)\)
\(\displaystyle \mathbf{\Phi}_{8} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(140 x y - 20 x + 210 y^{2} - 180 y + 20\right)&\displaystyle 10 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)\\\displaystyle 10 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)&\displaystyle y \left(- 140 x y^{2} + 180 x y - 40 x - 35 y^{3} + 100 y^{2} - 80 y + 16\right)\end{array}\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \mathbf{\Phi}_{8} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(140 x y - 20 x + 210 y^{2} - 180 y + 20\right)&\displaystyle 10 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)\\\displaystyle 10 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)&\displaystyle y \left(- 140 x y^{2} + 180 x y - 40 x - 35 y^{3} + 100 y^{2} - 80 y + 16\right)\end{array}\right)\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle l_{9}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{0}}(2 s_{0}^{2} - 3 s_{0} + 1)\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)\)
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{9} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} - 3 x^{2} - 42 x y^{2} + 24 x y - 5 x + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)\\\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)&\displaystyle 6 y \left(- 42 x^{2} y + 39 x^{2} + 24 x y - 26 x + 7 y^{3} - 16 y^{2} + 8 y + 1\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{9} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} - 3 x^{2} - 42 x y^{2} + 24 x y - 5 x + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)\\\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)&\displaystyle 6 y \left(- 42 x^{2} y + 39 x^{2} + 24 x y - 26 x + 7 y^{3} - 16 y^{2} + 8 y + 1\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{10}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{0}}(2 s_{0}^{2} - 3 s_{0} + 1)\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle \frac{\sqrt{2}}{2}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)\)
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{10} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} + 280 x^{2} y - 43 x^{2} + 378 x y^{2} - 336 x y + 35 x + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)\\\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)&\displaystyle 6 y \left(- 42 x^{2} y + 9 x^{2} - 280 x y^{2} + 384 x y - 86 x - 63 y^{3} + 184 y^{2} - 152 y + 31\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{10} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} + 280 x^{2} y - 43 x^{2} + 378 x y^{2} - 336 x y + 35 x + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)\\\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)&\displaystyle 6 y \left(- 42 x^{2} y + 9 x^{2} - 280 x y^{2} + 384 x y - 86 x - 63 y^{3} + 184 y^{2} - 152 y + 31\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{11}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{0}}(s_{0} \cdot \left(2 s_{0} - 1\right))\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)\)
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{11} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} - 8 x^{2} - 42 x y^{2} + 24 x y + 15 y^{2} - 10 y + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)\\\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)&\displaystyle 6 y \left(- 42 x^{2} y + 24 x^{2} + 24 x y - 16 x + 7 y^{3} - 11 y^{2} + 3 y + 1\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{11} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} - 8 x^{2} - 42 x y^{2} + 24 x y + 15 y^{2} - 10 y + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)\\\displaystyle 24 x y \left(- 7 x^{2} + 6 x + 7 y^{2} - 6 y\right)&\displaystyle 6 y \left(- 42 x^{2} y + 24 x^{2} + 24 x y - 16 x + 7 y^{3} - 11 y^{2} + 3 y + 1\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{12}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{0}}(s_{0} \cdot \left(2 s_{0} - 1\right))\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle \frac{\sqrt{2}}{2}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)\)
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{12} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} + 280 x^{2} y - 48 x^{2} + 378 x y^{2} - 336 x y + 40 x + 15 y^{2} - 10 y + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)\\\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)&\displaystyle 6 y \left(- 42 x^{2} y + 24 x^{2} - 280 x y^{2} + 384 x y - 96 x - 63 y^{3} + 179 y^{2} - 147 y + 31\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{12} = \left(\begin{array}{cc}\displaystyle 6 x \left(7 x^{3} + 280 x^{2} y - 48 x^{2} + 378 x y^{2} - 336 x y + 40 x + 15 y^{2} - 10 y + 1\right)&\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)\\\displaystyle 24 x y \left(- 7 x^{2} - 105 x y + 36 x - 63 y^{2} + 84 y - 20\right)&\displaystyle 6 y \left(- 42 x^{2} y + 24 x^{2} - 280 x y^{2} + 384 x y - 96 x - 63 y^{3} + 179 y^{2} - 147 y + 31\right)\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{13}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{0}}(4 s_{0} \cdot \left(1 - s_{0}\right))\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)\)
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{13} = \left(\begin{array}{cc}\displaystyle \frac{3 x \left(- 182 x^{3} - 2450 x^{2} y + 563 x^{2} - 3108 x y^{2} + 2856 x y - 385 x + 15 y^{2} - 20 y + 4\right)}{2}&\displaystyle \frac{3 x y \left(728 x^{2} + 3675 x y - 1674 x + 2072 y^{2} - 2826 y + 750\right)}{2}\\\displaystyle \frac{3 x y \left(728 x^{2} + 3675 x y - 1674 x + 2072 y^{2} - 2826 y + 750\right)}{2}&\displaystyle \frac{3 y \left(1092 x^{2} y - 609 x^{2} + 2450 x y^{2} - 3744 x y + 1096 x + 518 y^{3} - 1529 y^{2} + 1307 y - 296\right)}{2}\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{13} = \left(\begin{array}{cc}\displaystyle \frac{3 x \left(- 182 x^{3} - 2450 x^{2} y + 563 x^{2} - 3108 x y^{2} + 2856 x y - 385 x + 15 y^{2} - 20 y + 4\right)}{2}&\displaystyle \frac{3 x y \left(728 x^{2} + 3675 x y - 1674 x + 2072 y^{2} - 2826 y + 750\right)}{2}\\\displaystyle \frac{3 x y \left(728 x^{2} + 3675 x y - 1674 x + 2072 y^{2} - 2826 y + 750\right)}{2}&\displaystyle \frac{3 y \left(1092 x^{2} y - 609 x^{2} + 2450 x y^{2} - 3744 x y + 1096 x + 518 y^{3} - 1529 y^{2} + 1307 y - 296\right)}{2}\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{14}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{0}}(4 s_{0} \cdot \left(1 - s_{0}\right))\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle \frac{\sqrt{2}}{2}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle - \frac{\sqrt{2}}{2}\\\displaystyle - \frac{\sqrt{2}}{2}\end{array}\right)\)
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{14} = \left(\begin{array}{cc}\displaystyle \frac{3 x \left(- 7 x^{3} - 280 x^{2} y + 53 x^{2} - 378 x y^{2} + 366 x y - 50 x + 15 y^{2} - 20 y + 4\right)}{2}&\displaystyle 6 x y \left(7 x^{2} + 105 x y - 36 x + 63 y^{2} - 84 y + 20\right)\\\displaystyle 6 x y \left(7 x^{2} + 105 x y - 36 x + 63 y^{2} - 84 y + 20\right)&\displaystyle \frac{3 y \left(42 x^{2} y - 39 x^{2} + 280 x y^{2} - 414 x y + 116 x + 63 y^{3} - 189 y^{2} + 162 y - 36\right)}{2}\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \mathbf{\Phi}_{14} = \left(\begin{array}{cc}\displaystyle \frac{3 x \left(- 7 x^{3} - 280 x^{2} y + 53 x^{2} - 378 x y^{2} + 366 x y - 50 x + 15 y^{2} - 20 y + 4\right)}{2}&\displaystyle 6 x y \left(7 x^{2} + 105 x y - 36 x + 63 y^{2} - 84 y + 20\right)\\\displaystyle 6 x y \left(7 x^{2} + 105 x y - 36 x + 63 y^{2} - 84 y + 20\right)&\displaystyle \frac{3 y \left(42 x^{2} y - 39 x^{2} + 280 x y^{2} - 414 x y + 116 x + 63 y^{3} - 189 y^{2} + 162 y - 36\right)}{2}\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{15}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{1}}(2 s_{0}^{2} - 3 s_{0} + 1)\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{15} = \left(\begin{array}{cc}\displaystyle - 84 x^{4} - 1680 x^{3} y + 276 x^{3} - 2016 x^{2} y^{2} + 1692 x^{2} y - 120 x^{2} - 180 x y^{2} + 240 x y - 72 x - 420 y^{4} + 900 y^{3} - 600 y^{2} + 120 y&\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)\\\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)&\displaystyle 24 y \left(21 x^{2} y - 12 x^{2} + 70 x y^{2} - 102 x y + 28 x + 14 y^{3} - 42 y^{2} + 36 y - 8\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{15} = \left(\begin{array}{cc}\displaystyle - 84 x^{4} - 1680 x^{3} y + 276 x^{3} - 2016 x^{2} y^{2} + 1692 x^{2} y - 120 x^{2} - 180 x y^{2} + 240 x y - 72 x - 420 y^{4} + 900 y^{3} - 600 y^{2} + 120 y&\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)\\\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)&\displaystyle 24 y \left(21 x^{2} y - 12 x^{2} + 70 x y^{2} - 102 x y + 28 x + 14 y^{3} - 42 y^{2} + 36 y - 8\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{16}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{1}}(2 s_{0}^{2} - 3 s_{0} + 1)\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{16} = \left(\begin{array}{cc}\displaystyle 60 x \left(7 x^{3} + 112 x^{2} y - 23 x^{2} + 126 x y^{2} - 114 x y + 14 x - 28 y^{3} + 45 y^{2} - 20 y + 2\right)&\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 69 x^{2} - 84 x y^{2} + 114 x y - 28 x + 7 y^{3} - 15 y^{2} + 10 y - 2\right)\\\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 69 x^{2} - 84 x y^{2} + 114 x y - 28 x + 7 y^{3} - 15 y^{2} + 10 y - 2\right)&\displaystyle 60 y \left(- 42 x^{2} y + 27 x^{2} - 112 x y^{2} + 174 x y - 52 x - 21 y^{3} + 67 y^{2} - 60 y + 14\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{16} = \left(\begin{array}{cc}\displaystyle 60 x \left(7 x^{3} + 112 x^{2} y - 23 x^{2} + 126 x y^{2} - 114 x y + 14 x - 28 y^{3} + 45 y^{2} - 20 y + 2\right)&\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 69 x^{2} - 84 x y^{2} + 114 x y - 28 x + 7 y^{3} - 15 y^{2} + 10 y - 2\right)\\\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 69 x^{2} - 84 x y^{2} + 114 x y - 28 x + 7 y^{3} - 15 y^{2} + 10 y - 2\right)&\displaystyle 60 y \left(- 42 x^{2} y + 27 x^{2} - 112 x y^{2} + 174 x y - 52 x - 21 y^{3} + 67 y^{2} - 60 y + 14\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{17}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{1}}(s_{0} \cdot \left(2 s_{0} - 1\right))\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{17} = \left(\begin{array}{cc}\displaystyle - 84 x^{4} - 1680 x^{3} y + 336 x^{3} - 2016 x^{2} y^{2} + 1872 x^{2} y - 240 x^{2} - 180 x y^{2} + 120 x y - 12 x - 420 y^{4} + 780 y^{3} - 420 y^{2} + 60 y&\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)\\\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)&\displaystyle 24 y \left(21 x^{2} y - 12 x^{2} + 70 x y^{2} - 102 x y + 28 x + 14 y^{3} - 42 y^{2} + 36 y - 8\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{17} = \left(\begin{array}{cc}\displaystyle - 84 x^{4} - 1680 x^{3} y + 336 x^{3} - 2016 x^{2} y^{2} + 1872 x^{2} y - 240 x^{2} - 180 x y^{2} + 120 x y - 12 x - 420 y^{4} + 780 y^{3} - 420 y^{2} + 60 y&\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)\\\displaystyle 24 x y \left(14 x^{2} + 105 x y - 42 x + 56 y^{2} - 78 y + 20\right)&\displaystyle 24 y \left(21 x^{2} y - 12 x^{2} + 70 x y^{2} - 102 x y + 28 x + 14 y^{3} - 42 y^{2} + 36 y - 8\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{18}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{1}}(s_{0} \cdot \left(2 s_{0} - 1\right))\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{18} = \left(\begin{array}{cc}\displaystyle 60 x \left(7 x^{3} + 112 x^{2} y - 24 x^{2} + 126 x y^{2} - 120 x y + 16 x - 28 y^{3} + 39 y^{2} - 14 y + 1\right)&\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 72 x^{2} - 84 x y^{2} + 120 x y - 32 x + 7 y^{3} - 13 y^{2} + 7 y - 1\right)\\\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 72 x^{2} - 84 x y^{2} + 120 x y - 32 x + 7 y^{3} - 13 y^{2} + 7 y - 1\right)&\displaystyle 60 y \left(- 42 x^{2} y + 24 x^{2} - 112 x y^{2} + 168 x y - 48 x - 21 y^{3} + 65 y^{2} - 57 y + 13\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{18} = \left(\begin{array}{cc}\displaystyle 60 x \left(7 x^{3} + 112 x^{2} y - 24 x^{2} + 126 x y^{2} - 120 x y + 16 x - 28 y^{3} + 39 y^{2} - 14 y + 1\right)&\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 72 x^{2} - 84 x y^{2} + 120 x y - 32 x + 7 y^{3} - 13 y^{2} + 7 y - 1\right)\\\displaystyle 60 y \left(- 28 x^{3} - 168 x^{2} y + 72 x^{2} - 84 x y^{2} + 120 x y - 32 x + 7 y^{3} - 13 y^{2} + 7 y - 1\right)&\displaystyle 60 y \left(- 42 x^{2} y + 24 x^{2} - 112 x y^{2} + 168 x y - 48 x - 21 y^{3} + 65 y^{2} - 57 y + 13\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{19}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{1}}(4 s_{0} \cdot \left(1 - s_{0}\right))\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{19} = \left(\begin{array}{cc}\displaystyle - \frac{483 x^{4}}{2} - 3255 x^{3} y + 726 x^{3} - 4221 x^{2} y^{2} + 3852 x^{2} y - \frac{975 x^{2}}{2} + 90 x y^{2} - 90 x y + 3 x + 105 y^{4} - 210 y^{3} + 120 y^{2} - 15 y&\displaystyle \frac{3 x y \left(644 x^{2} + 3255 x y - 1482 x + 1876 y^{2} - 2538 y + 670\right)}{2}\\\displaystyle \frac{3 x y \left(644 x^{2} + 3255 x y - 1482 x + 1876 y^{2} - 2538 y + 670\right)}{2}&\displaystyle \frac{3 y \left(966 x^{2} y - 552 x^{2} + 2170 x y^{2} - 3342 x y + 988 x + 469 y^{3} - 1382 y^{2} + 1181 y - 268\right)}{2}\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{19} = \left(\begin{array}{cc}\displaystyle - \frac{483 x^{4}}{2} - 3255 x^{3} y + 726 x^{3} - 4221 x^{2} y^{2} + 3852 x^{2} y - \frac{975 x^{2}}{2} + 90 x y^{2} - 90 x y + 3 x + 105 y^{4} - 210 y^{3} + 120 y^{2} - 15 y&\displaystyle \frac{3 x y \left(644 x^{2} + 3255 x y - 1482 x + 1876 y^{2} - 2538 y + 670\right)}{2}\\\displaystyle \frac{3 x y \left(644 x^{2} + 3255 x y - 1482 x + 1876 y^{2} - 2538 y + 670\right)}{2}&\displaystyle \frac{3 y \left(966 x^{2} y - 552 x^{2} + 2170 x y^{2} - 3342 x y + 988 x + 469 y^{3} - 1382 y^{2} + 1181 y - 268\right)}{2}\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{20}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{1}}(4 s_{0} \cdot \left(1 - s_{0}\right))\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{20} = \left(\begin{array}{cc}\displaystyle 15 x \left(- 7 x^{3} - 112 x^{2} y + 25 x^{2} - 126 x y^{2} + 120 x y - 17 x + 28 y^{3} - 42 y^{2} + 16 y - 1\right)&\displaystyle 15 y \left(28 x^{3} + 168 x^{2} y - 75 x^{2} + 84 x y^{2} - 120 x y + 34 x - 7 y^{3} + 14 y^{2} - 8 y + 1\right)\\\displaystyle 15 y \left(28 x^{3} + 168 x^{2} y - 75 x^{2} + 84 x y^{2} - 120 x y + 34 x - 7 y^{3} + 14 y^{2} - 8 y + 1\right)&\displaystyle 15 y \left(42 x^{2} y - 21 x^{2} + 112 x y^{2} - 168 x y + 46 x + 21 y^{3} - 66 y^{2} + 58 y - 13\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \mathbf{\Phi}_{20} = \left(\begin{array}{cc}\displaystyle 15 x \left(- 7 x^{3} - 112 x^{2} y + 25 x^{2} - 126 x y^{2} + 120 x y - 17 x + 28 y^{3} - 42 y^{2} + 16 y - 1\right)&\displaystyle 15 y \left(28 x^{3} + 168 x^{2} y - 75 x^{2} + 84 x y^{2} - 120 x y + 34 x - 7 y^{3} + 14 y^{2} - 8 y + 1\right)\\\displaystyle 15 y \left(28 x^{3} + 168 x^{2} y - 75 x^{2} + 84 x y^{2} - 120 x y + 34 x - 7 y^{3} + 14 y^{2} - 8 y + 1\right)&\displaystyle 15 y \left(42 x^{2} y - 21 x^{2} + 112 x y^{2} - 168 x y + 46 x + 21 y^{3} - 66 y^{2} + 58 y - 13\right)\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{21}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{2}}(2 s_{0}^{2} - 3 s_{0} + 1)\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{21} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(1680 x y - 240 x + 2520 y^{2} - 2160 y + 240\right)&\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)\\\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)&\displaystyle - 420 x^{4} + 900 x^{3} - 180 x^{2} y - 600 x^{2} - 1680 x y^{3} + 1980 x y^{2} - 240 x y + 120 x - 420 y^{4} + 1140 y^{3} - 840 y^{2} + 120 y\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{21} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(1680 x y - 240 x + 2520 y^{2} - 2160 y + 240\right)&\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)\\\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)&\displaystyle - 420 x^{4} + 900 x^{3} - 180 x^{2} y - 600 x^{2} - 1680 x y^{3} + 1980 x y^{2} - 240 x y + 120 x - 420 y^{4} + 1140 y^{3} - 840 y^{2} + 120 y\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{22}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{2}}(2 s_{0}^{2} - 3 s_{0} + 1)\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{22} = \left(\begin{array}{cc}\displaystyle 12 x \left(- 7 x^{3} + 560 x^{2} y - 87 x^{2} + 882 x y^{2} - 774 x y + 100 x - 15 y^{2} + 20 y - 6\right)&\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 75 x^{2} - 840 x y^{2} + 246 x y - 50 x - 588 y^{3} + 759 y^{2} - 180 y + 10\right)\\\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 75 x^{2} - 840 x y^{2} + 246 x y - 50 x - 588 y^{3} + 759 y^{2} - 180 y + 10\right)&\displaystyle 12 y \left(140 x^{3} + 42 x^{2} y - 249 x^{2} - 560 x y^{2} + 666 x y - 44 x - 147 y^{3} + 411 y^{2} - 318 y + 54\right)\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{22} = \left(\begin{array}{cc}\displaystyle 12 x \left(- 7 x^{3} + 560 x^{2} y - 87 x^{2} + 882 x y^{2} - 774 x y + 100 x - 15 y^{2} + 20 y - 6\right)&\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 75 x^{2} - 840 x y^{2} + 246 x y - 50 x - 588 y^{3} + 759 y^{2} - 180 y + 10\right)\\\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 75 x^{2} - 840 x y^{2} + 246 x y - 50 x - 588 y^{3} + 759 y^{2} - 180 y + 10\right)&\displaystyle 12 y \left(140 x^{3} + 42 x^{2} y - 249 x^{2} - 560 x y^{2} + 666 x y - 44 x - 147 y^{3} + 411 y^{2} - 318 y + 54\right)\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{23}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{2}}(s_{0} \cdot \left(2 s_{0} - 1\right))\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{23} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(1680 x y - 240 x + 2520 y^{2} - 2160 y + 240\right)&\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)\\\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)&\displaystyle - 420 x^{4} + 780 x^{3} - 180 x^{2} y - 420 x^{2} - 1680 x y^{3} + 2160 x y^{2} - 360 x y + 60 x - 420 y^{4} + 1200 y^{3} - 960 y^{2} + 180 y\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{23} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(1680 x y - 240 x + 2520 y^{2} - 2160 y + 240\right)&\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)\\\displaystyle 120 x y \left(- 21 x y + 6 x - 14 y^{2} + 18 y - 4\right)&\displaystyle - 420 x^{4} + 780 x^{3} - 180 x^{2} y - 420 x^{2} - 1680 x y^{3} + 2160 x y^{2} - 360 x y + 60 x - 420 y^{4} + 1200 y^{3} - 960 y^{2} + 180 y\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{24}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{2}}(s_{0} \cdot \left(2 s_{0} - 1\right))\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{24} = \left(\begin{array}{cc}\displaystyle 12 x \left(- 7 x^{3} + 560 x^{2} y - 77 x^{2} + 882 x y^{2} - 744 x y + 85 x - 1\right)&\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 65 x^{2} - 840 x y^{2} + 216 x y - 35 x - 588 y^{3} + 744 y^{2} - 160 y + 5\right)\\\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 65 x^{2} - 840 x y^{2} + 216 x y - 35 x - 588 y^{3} + 744 y^{2} - 160 y + 5\right)&\displaystyle 12 y \left(140 x^{3} + 42 x^{2} y - 219 x^{2} - 560 x y^{2} + 696 x y - 74 x - 147 y^{3} + 416 y^{2} - 328 y + 59\right)\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{24} = \left(\begin{array}{cc}\displaystyle 12 x \left(- 7 x^{3} + 560 x^{2} y - 77 x^{2} + 882 x y^{2} - 744 x y + 85 x - 1\right)&\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 65 x^{2} - 840 x y^{2} + 216 x y - 35 x - 588 y^{3} + 744 y^{2} - 160 y + 5\right)\\\displaystyle 12 x \left(- 35 x^{3} + 28 x^{2} y + 65 x^{2} - 840 x y^{2} + 216 x y - 35 x - 588 y^{3} + 744 y^{2} - 160 y + 5\right)&\displaystyle 12 y \left(140 x^{3} + 42 x^{2} y - 219 x^{2} - 560 x y^{2} + 696 x y - 74 x - 147 y^{3} + 416 y^{2} - 328 y + 59\right)\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{25}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{2}}(4 s_{0} \cdot \left(1 - s_{0}\right))\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{25} = \left(\begin{array}{cc}\displaystyle \frac{15 x^{2} \left(- 35 x^{2} - 546 x y + 118 x - 714 y^{2} + 642 y - 83\right)}{2}&\displaystyle \frac{15 x y \left(140 x^{2} + 819 x y - 354 x + 476 y^{2} - 642 y + 166\right)}{2}\\\displaystyle \frac{15 x y \left(140 x^{2} + 819 x y - 354 x + 476 y^{2} - 642 y + 166\right)}{2}&\displaystyle 105 x^{4} - 210 x^{3} + 1575 x^{2} y^{2} - 810 x^{2} y + 120 x^{2} + 4095 x y^{3} - 6120 x y^{2} + 1680 x y - 15 x + \frac{1785 y^{4}}{2} - 2640 y^{3} + \frac{4485 y^{2}}{2} - 495 y\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{25} = \left(\begin{array}{cc}\displaystyle \frac{15 x^{2} \left(- 35 x^{2} - 546 x y + 118 x - 714 y^{2} + 642 y - 83\right)}{2}&\displaystyle \frac{15 x y \left(140 x^{2} + 819 x y - 354 x + 476 y^{2} - 642 y + 166\right)}{2}\\\displaystyle \frac{15 x y \left(140 x^{2} + 819 x y - 354 x + 476 y^{2} - 642 y + 166\right)}{2}&\displaystyle 105 x^{4} - 210 x^{3} + 1575 x^{2} y^{2} - 810 x^{2} y + 120 x^{2} + 4095 x y^{3} - 6120 x y^{2} + 1680 x y - 15 x + \frac{1785 y^{4}}{2} - 2640 y^{3} + \frac{4485 y^{2}}{2} - 495 y\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{26}:\boldsymbol{V}\mapsto\displaystyle\int_{e_{2}}(4 s_{0} \cdot \left(1 - s_{0}\right))\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{26} = \left(\begin{array}{cc}\displaystyle 3 x \left(7 x^{3} - 560 x^{2} y + 82 x^{2} - 882 x y^{2} + 744 x y - 90 x - 15 y^{2} + 10 y + 1\right)&\displaystyle 3 x \left(35 x^{3} - 28 x^{2} y - 70 x^{2} + 840 x y^{2} - 216 x y + 40 x + 588 y^{3} - 729 y^{2} + 150 y - 5\right)\\\displaystyle 3 x \left(35 x^{3} - 28 x^{2} y - 70 x^{2} + 840 x y^{2} - 216 x y + 40 x + 588 y^{3} - 729 y^{2} + 150 y - 5\right)&\displaystyle 3 y \left(- 140 x^{3} - 42 x^{2} y + 234 x^{2} + 560 x y^{2} - 696 x y + 64 x + 147 y^{3} - 421 y^{2} + 333 y - 59\right)\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \mathbf{\Phi}_{26} = \left(\begin{array}{cc}\displaystyle 3 x \left(7 x^{3} - 560 x^{2} y + 82 x^{2} - 882 x y^{2} + 744 x y - 90 x - 15 y^{2} + 10 y + 1\right)&\displaystyle 3 x \left(35 x^{3} - 28 x^{2} y - 70 x^{2} + 840 x y^{2} - 216 x y + 40 x + 588 y^{3} - 729 y^{2} + 150 y - 5\right)\\\displaystyle 3 x \left(35 x^{3} - 28 x^{2} y - 70 x^{2} + 840 x y^{2} - 216 x y + 40 x + 588 y^{3} - 729 y^{2} + 150 y - 5\right)&\displaystyle 3 y \left(- 140 x^{3} - 42 x^{2} y + 234 x^{2} + 560 x y^{2} - 696 x y + 64 x + 147 y^{3} - 421 y^{2} + 333 y - 59\right)\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{27}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle - s_{0} - s_{1} + 1&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{27} = \left(\begin{array}{cc}\displaystyle 120 x \left(3 x^{2} + 6 x y - 5 x + 3 y^{2} - 5 y + 2\right)&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{27} = \left(\begin{array}{cc}\displaystyle 120 x \left(3 x^{2} + 6 x y - 5 x + 3 y^{2} - 5 y + 2\right)&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{28}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 0&\displaystyle - s_{0} - s_{1} + 1\\\displaystyle 0&\displaystyle 0\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{28} = \left(\begin{array}{cc}\displaystyle 60 x \left(- 35 x^{3} - 490 x^{2} y + 116 x^{2} - 630 x y^{2} + 594 x y - 85 x + 18 y^{2} - 20 y + 4\right)&\displaystyle 60 x y \left(140 x^{2} + 735 x y - 342 x + 420 y^{2} - 582 y + 160\right)\\\displaystyle 60 x y \left(140 x^{2} + 735 x y - 342 x + 420 y^{2} - 582 y + 160\right)&\displaystyle 60 y \left(210 x^{2} y - 102 x^{2} + 490 x y^{2} - 726 x y + 200 x + 105 y^{3} - 304 y^{2} + 255 y - 56\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{28} = \left(\begin{array}{cc}\displaystyle 60 x \left(- 35 x^{3} - 490 x^{2} y + 116 x^{2} - 630 x y^{2} + 594 x y - 85 x + 18 y^{2} - 20 y + 4\right)&\displaystyle 60 x y \left(140 x^{2} + 735 x y - 342 x + 420 y^{2} - 582 y + 160\right)\\\displaystyle 60 x y \left(140 x^{2} + 735 x y - 342 x + 420 y^{2} - 582 y + 160\right)&\displaystyle 60 y \left(210 x^{2} y - 102 x^{2} + 490 x y^{2} - 726 x y + 200 x + 105 y^{3} - 304 y^{2} + 255 y - 56\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{29}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle - s_{0} - s_{1} + 1\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{29} = \left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 120 y \left(3 x^{2} + 6 x y - 5 x + 3 y^{2} - 5 y + 2\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{29} = \left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 120 y \left(3 x^{2} + 6 x y - 5 x + 3 y^{2} - 5 y + 2\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{30}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle s_{0}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{30} = \left(\begin{array}{cc}\displaystyle 120 x \left(- 3 x^{2} - 3 x y + 4 x + y - 1\right)&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{30} = \left(\begin{array}{cc}\displaystyle 120 x \left(- 3 x^{2} - 3 x y + 4 x + y - 1\right)&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{31}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 0&\displaystyle s_{0}\\\displaystyle 0&\displaystyle 0\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{31} = \left(\begin{array}{cc}\displaystyle 60 x \left(35 x^{3} + 490 x^{2} y - 116 x^{2} + 630 x y^{2} - 582 x y + 83 x + 4 y - 2\right)&\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 336 x - 420 y^{2} + 570 y - 152\right)\\\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 336 x - 420 y^{2} + 570 y - 152\right)&\displaystyle 60 y \left(- 210 x^{2} y + 102 x^{2} - 490 x y^{2} + 738 x y - 204 x - 105 y^{3} + 310 y^{2} - 263 y + 58\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{31} = \left(\begin{array}{cc}\displaystyle 60 x \left(35 x^{3} + 490 x^{2} y - 116 x^{2} + 630 x y^{2} - 582 x y + 83 x + 4 y - 2\right)&\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 336 x - 420 y^{2} + 570 y - 152\right)\\\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 336 x - 420 y^{2} + 570 y - 152\right)&\displaystyle 60 y \left(- 210 x^{2} y + 102 x^{2} - 490 x y^{2} + 738 x y - 204 x - 105 y^{3} + 310 y^{2} - 263 y + 58\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{32}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle s_{0}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{32} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(2100 x^{2} + 29400 x y - 6600 x + 37800 y^{2} - 34200 y + 4500\right)&\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)\\\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)&\displaystyle 60 y \left(- 210 x^{2} y + 108 x^{2} - 490 x y^{2} + 738 x y - 206 x - 105 y^{3} + 310 y^{2} - 263 y + 58\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{32} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(2100 x^{2} + 29400 x y - 6600 x + 37800 y^{2} - 34200 y + 4500\right)&\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)\\\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)&\displaystyle 60 y \left(- 210 x^{2} y + 108 x^{2} - 490 x y^{2} + 738 x y - 206 x - 105 y^{3} + 310 y^{2} - 263 y + 58\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{33}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle s_{1}&\displaystyle 0\\\displaystyle 0&\displaystyle 0\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{33} = \left(\begin{array}{cc}\displaystyle 60 x \left(35 x^{3} + 490 x^{2} y - 110 x^{2} + 630 x y^{2} - 582 x y + 77 x - 12 y^{2} + 14 y - 2\right)&\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)\\\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)&\displaystyle 300 y \left(- 42 x^{2} y + 24 x^{2} - 98 x y^{2} + 150 x y - 44 x - 21 y^{3} + 62 y^{2} - 53 y + 12\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{33} = \left(\begin{array}{cc}\displaystyle 60 x \left(35 x^{3} + 490 x^{2} y - 110 x^{2} + 630 x y^{2} - 582 x y + 77 x - 12 y^{2} + 14 y - 2\right)&\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)\\\displaystyle 300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)&\displaystyle 300 y \left(- 42 x^{2} y + 24 x^{2} - 98 x y^{2} + 150 x y - 44 x - 21 y^{3} + 62 y^{2} - 53 y + 12\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{34}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 0&\displaystyle s_{1}\\\displaystyle 0&\displaystyle 0\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{34} = \left(\begin{array}{cc}\displaystyle 60 x \left(35 x^{3} + 490 x^{2} y - 110 x^{2} + 630 x y^{2} - 582 x y + 77 x - 18 y^{2} + 16 y - 2\right)&\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 330 x - 420 y^{2} + 576 y - 152\right)\\\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 330 x - 420 y^{2} + 576 y - 152\right)&\displaystyle 60 y \left(- 210 x^{2} y + 120 x^{2} - 490 x y^{2} + 738 x y - 216 x - 105 y^{3} + 304 y^{2} - 257 y + 58\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{34} = \left(\begin{array}{cc}\displaystyle 60 x \left(35 x^{3} + 490 x^{2} y - 110 x^{2} + 630 x y^{2} - 582 x y + 77 x - 18 y^{2} + 16 y - 2\right)&\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 330 x - 420 y^{2} + 576 y - 152\right)\\\displaystyle 60 x y \left(- 140 x^{2} - 735 x y + 330 x - 420 y^{2} + 576 y - 152\right)&\displaystyle 60 y \left(- 210 x^{2} y + 120 x^{2} - 490 x y^{2} + 738 x y - 216 x - 105 y^{3} + 304 y^{2} - 257 y + 58\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{35}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle s_{1}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{35} = \left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 120 y \left(- 3 x y + x - 3 y^{2} + 4 y - 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{35} = \left(\begin{array}{cc}\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 120 y \left(- 3 x y + x - 3 y^{2} + 4 y - 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{36}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{cc}\displaystyle 2 s_{1}^{2} \cdot \left(6 s_{0}^{2} + 6 s_{0} s_{1} - 6 s_{0} + s_{1}^{2} - 2 s_{1} + 1\right)&\displaystyle 2 s_{0} s_{1} \cdot \left(4 s_{0}^{2} + 9 s_{0} s_{1} - 6 s_{0} + 4 s_{1}^{2} - 6 s_{1} + 2\right)\\\displaystyle 2 s_{0} s_{1} \cdot \left(4 s_{0}^{2} + 9 s_{0} s_{1} - 6 s_{0} + 4 s_{1}^{2} - 6 s_{1} + 2\right)&\displaystyle 2 s_{0}^{2} \left(s_{0}^{2} + 6 s_{0} s_{1} - 2 s_{0} + 6 s_{1}^{2} - 6 s_{1} + 1\right)\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{36} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(44100 x^{2} + 617400 x y - 138600 x + 793800 y^{2} - 718200 y + 94500\right)&\displaystyle 6300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)\\\displaystyle 6300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)&\displaystyle 6300 y \left(- 42 x^{2} y + 24 x^{2} - 98 x y^{2} + 150 x y - 44 x - 21 y^{3} + 62 y^{2} - 53 y + 12\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{36} = \left(\begin{array}{cc}\displaystyle x^{2} \cdot \left(44100 x^{2} + 617400 x y - 138600 x + 793800 y^{2} - 718200 y + 94500\right)&\displaystyle 6300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)\\\displaystyle 6300 x y \left(- 28 x^{2} - 147 x y + 66 x - 84 y^{2} + 114 y - 30\right)&\displaystyle 6300 y \left(- 42 x^{2} y + 24 x^{2} - 98 x y^{2} + 150 x y - 44 x - 21 y^{3} + 62 y^{2} - 53 y + 12\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference element.