an encyclopedia of finite element definitions
Degree 1 enriched vector Galerkin on a hexahedron
◀ Back to enriched vector Galerkin definition page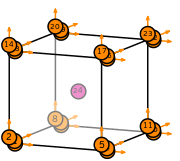
- \(R\) is the reference hexahedron. The following numbering of the subentities of the reference is used:
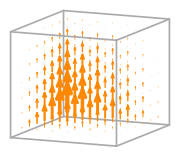
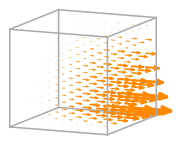
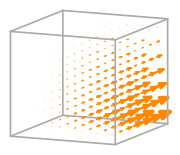
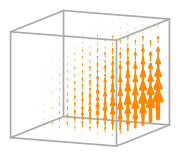
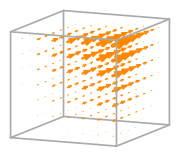
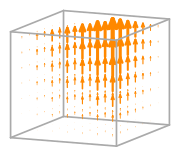
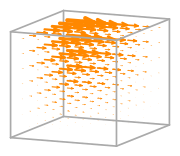
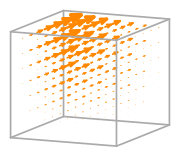
- Basis functions:

\(\displaystyle \boldsymbol{\phi}_{0} = \left(\begin{array}{c}\displaystyle - x y z + x y + x z - x + y z - y - z + 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{1} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle - x y z + x y + x z - x + y z - y - z + 1\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{2} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - x y z + x y + x z - x + y z - y - z + 1\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{3} = \left(\begin{array}{c}\displaystyle x \left(y z - y - z + 1\right)\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{4} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle x \left(y z - y - z + 1\right)\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{5} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x \left(y z - y - z + 1\right)\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{6} = \left(\begin{array}{c}\displaystyle y \left(x z - x - z + 1\right)\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{7} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle y \left(x z - x - z + 1\right)\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{8} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y \left(x z - x - z + 1\right)\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{9} = \left(\begin{array}{c}\displaystyle x y \left(1 - z\right)\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{10} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle x y \left(1 - z\right)\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{11} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x y \left(1 - z\right)\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{12} = \left(\begin{array}{c}\displaystyle z \left(x y - x - y + 1\right)\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{13} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle z \left(x y - x - y + 1\right)\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{14} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle z \left(x y - x - y + 1\right)\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{15} = \left(\begin{array}{c}\displaystyle x z \left(1 - y\right)\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{16} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle x z \left(1 - y\right)\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{17} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x z \left(1 - y\right)\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{18} = \left(\begin{array}{c}\displaystyle y z \left(1 - x\right)\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{19} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle y z \left(1 - x\right)\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{20} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y z \left(1 - x\right)\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{21} = \left(\begin{array}{c}\displaystyle x y z\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{22} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle x y z\\\displaystyle 0\end{array}\right)\)
\(\displaystyle \boldsymbol{\phi}_{23} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x y z\end{array}\right)\)